光とは
光は、相対性理論において特に重要な概念ですので、改めて説明します。
1.光の種類
光は広義には電磁波をいいますが、狭義には電磁波のうち人間の視覚で認識できる波長(380nm〜760nm)のものをいいます。
電磁波は主として波長により表1のとおり分類されています。
なお、相対性理論における説明においては、特に断らない限り「光」は電磁波をいうものとします。
| γ線 | 3x1016Hz以上 |
| X線 | |
| 紫外線 | 3x1015〜16Hz |
| 可視光線 | 3x1013〜15Hz |
| 赤外線 | 3x1012〜13Hz |
| サブミリ波 | 3x1011〜12Hz |
| マイクロ波 | 3x108〜11Hz |
| 超音波 | 3x107〜8Hz |
| 短波 | 3x106〜7Hz |
| 中波 | 3x105〜6Hz |
| 長波 | 3x104〜5Hz |
| 超長波 | 3x103〜4Hz |
| 極超長波 | 3x102〜3Hz |
| 極低周波 | 1〜300Hz |
2.光の性質と論争
光は表2に示されるような基本的性質を持っています。
| 直進 | 光は均質媒質中では直進する。 |
| 反射・屈折 | 光は異なる媒質の境界面でが反射又は屈折する。 |
| 通過・吸収 | 光が透明な媒質の内部を通過するときは、その通過する媒質内で光が吸収される。 |
| 干渉 | 位相差が時間とともに変化しない同一周波数の2つの光波が重なり合うことにより強め合い又は弱め合う(干渉する)。 |
| 回折 | 光が伝搬するときに障害物の背後の回り込むこと(回折)ができる。 |
これらの光の性質のうち、例えば干渉や回折は光が波動でなければ起こり得ない現象であるため、古くから光は波動であると考えられていました。
しかし、ニュートンの古典物理学の時代には、波動は媒質(水面波の水、音波の空気、圧力波の固体等)の存在が前提となるため、
真空の宇宙空間を光波の伝搬を説明するために宇宙空間に「エーテル」が充満しているとして説明していましたが、
19世紀末頃までにエーテルの存在を実証できるような現象が見つかりませんでした。
また、19世紀末頃までに以下のような光の粒子性を示す現象が発見されていたため、
光が波動なのか粒子なのかが物理学において議論となっていました。
①日焼け現象
光が波であるとすれば、光のエネルギーは光波の振幅の2乗に比例することになるため、
太陽光からの紫外線と同程度の強さのエネルギーの可視光を照射できる電球を準備して人体に照射すれば、
日焼けができるはずですが、そのような電球により日焼けは起こりませんでした。
一方、光が粒子であり、波長又は振動数に対応したエネルギーを持っていると考えれば、
可視光ではなく紫外線で照射しなければ日焼けが発生しないことが説明できます。
具体的には、周波数νの光は\(h\)νのエネルギー(\(h\)=プランク定数6.626x10-34J•s)を持っており、
紫外線の周波数は可視光線の周波数より2桁程度大きいため、光線のエネルギーの相違も同様です。
②光電効果
光電効果は、1887年に電磁波の実験中にヘルツによって発見された現象であり、
金属板表面に周波数νの光を照射すると、その照射光の周波数νが金属ごとに特定の周波数ν0より大きければ、
金属板が光を吸収して電子(「光電子」という。)を放出するが、νがν0より小さければ照射光の強さを高めても
光電子を放出しないというものです。
アインシュタインは、特殊相対性理論の論文を発表した1905年に、
この光電効果に関して光の粒子性を論証した「光量子仮説」としての論文発表を行い、
(特殊相対性理論ではなく)この論文によりノーベル賞を受賞しています。
3.電磁波の方程式
19世紀、電磁気学の発展により電磁場理論が整備され、電磁波の方程式、光速cが理論的に導かれました。
(1)Maxwellの方程式
\(\bm{E}\)、\(\bm{D}\)、\(\bm{H}\)、\(\bm{B}\)をそれぞれ、電場の強さ(電界強度)、電束密度、磁場の強さ(磁界強度)、磁束密度とし、 \(ε_{0}\)、\(μ_{0}\)をそれぞれ真空の誘電率、透磁率とすると、次の関係式が成り立ちます。 \begin{equation} \bm{D} = ε_{0} \bm{E} \label{1-1} \end{equation} \begin{equation} \bm{B} = μ_{0} \bm{H} \label{1-2} \end{equation} また、\(ρ\)、\(σ\)、\(\bm{j}\)(\(=σ\bm{E}\))をそれぞれ電荷密度、導電率、電流密度とすると、 次の4つの方程式を合わせたマクスウエルの方程式が成立します。
【誘電体内におけるガウスの定理】 \begin{equation} \mathrm{div} \bm{D} = ρ \label{1-3} \end{equation} 【真磁価の不存在】 \begin{equation} \mathrm{div} \bm{B} = 0 \label{1-4} \end{equation} 【ファラデーの電磁誘導の法則】 \begin{equation} \mathrm{rot} \bm{E} = -\dd{\bm{B}}{t} \label{1-5} \end{equation} 【拡張されたアンペールの法則】 \begin{equation} \mathrm{rot} \bm{H} = \bm{j} + \dd{\bm{D}}{t} \label{1-6} \end{equation}
【ベクトルの微分】
\(x\)軸、\(y\)軸、\(z\)軸方向の単位ベクトルをそれぞれ\(\bm{e_{x}}\)、 \(\bm{e_{y}}\)、\(\bm{e_{z}}\)とします。
ベクトルのスカラーでの微分
\(
\cfrac{\partial \bm{B}}{\partial t} = \bm{e_{x}}\cfrac{\partial B_{x}}{\partial t} + \bm{e_{y}}\cfrac{\partial B_{y}}{\partial t}
+ \bm{e_{z}}\cfrac{\partial B_{z}}{\partial t}
\)
発散
\(
\mathrm{div} \bm{D} = \cfrac{\partial D_{x}}{\partial x} + \cfrac{\partial D_{y}}{\partial y} + \cfrac{\partial D_{z}}{\partial z}
\)
回転
\(
\mathrm{rot} \bm{E} =
\begin{vmatrix}
\bm{e_{x}} & \bm{e_{y}} & \bm{e_{z}}\\
\cfrac{\partial}{\partial x} & \cfrac{\partial}{\partial y} & \cfrac{\partial}{\partial z}\\
E_{x} & E_{y} & E_{z}
\end{vmatrix}
\)
(2)電磁波の方程式の導出
電荷が存在せず(\(ρ=0\))、絶縁物(\(σ=0\))である真空空間において、
時間的に変化する電場\(\bm{B}\)と磁場\(\bm{B}\)が存在すると仮定し、
\eqref{1-1}と\eqref{1-2}を考慮するとマクスウエルの方程式は次式となります。
【誘電体内におけるガウスの定理】 \begin{equation} \mathrm{div} \bm{E} = 0 \label{1-7} \end{equation} 【真磁価の不存在】 \begin{equation} \mathrm{div} \bm{B} = 0 \label{1-8} \end{equation} 【ファラデーの電磁誘導の法則】 \begin{equation} \mathrm{rot} \bm{E} = -μ_{0}\dd{\bm{H}}{t} \label{1-9} \end{equation} 【拡張されたアンペールの法則】 \begin{equation} \mathrm{rot} \bm{H} = ε_{0}\dd{\bm{E}}{t} \label{1-10} \end{equation} ここで、簡単のため、電場\(\bm{E}\)と磁場\(\bm{H}\)は\(y\)と\(z\)に依存しない\(x\)だけの関数とすると、 \(\bm{E}(x,t)\)、\(\bm{H}(x,t)\)と表せるため、\eqref{1-7}、\eqref{1-8}はそれぞれ \begin{equation} \dd{E_{x}}{x} = 0 \label{1-11} \end{equation} \begin{equation} \dd{H_{x}}{x} = 0 \label{1-12} \end{equation} となり、\eqref{1-9}、\eqref{1-10}式はそれぞれ次式のようになります。 \begin{equation} \begin{pmatrix} 0\\ -\ \cfrac{\partial E_{z}}{\partial x}\\ \cfrac{\partial E_{y}}{\partial x}\\ \end{pmatrix} = \begin{pmatrix} -μ_{0}\cfrac{\partial H_{x}}{\partial t}\\ -μ_{0}\cfrac{\partial H_{y}}{\partial t}\\ -μ_{0}\cfrac{\partial H_{z}}{\partial t}\\ \end{pmatrix} \label{1-13} \end{equation} \begin{equation} \begin{pmatrix} 0\\ -\ \cfrac{\partial H_{z}}{\partial x}\\ \cfrac{\partial H_{y}}{\partial x}\\ \end{pmatrix} = \begin{pmatrix} ε_{0}\cfrac{\partial E_{x}}{\partial t}\\ ε_{0}\cfrac{\partial E_{y}}{\partial t}\\ ε_{0}\cfrac{\partial E_{z}}{\partial t}\\ \end{pmatrix} \label{1-14} \end{equation} \eqref{1-13}の両辺の第3成分を\(x\)で微分、\eqref{1-14}の両辺の第2成分を\(t\)で微分すると、それぞれ次式が得られます。 \begin{equation} \frac{\partial^2 E_{y}}{\partial x^2} = -μ_{0}\require{physics} \pdv{H_{z}}{x}{t} \label{1-15} \end{equation} \begin{equation} -\ \require{physics} \pdv{H_{z}}{t}{x} = ε_{0}\frac{\partial^2 E_{y}}{\partial t^2} \label{1-16} \end{equation} これら両式より電場\(E_{y}\)に関する次式が得られます。 \begin{equation} \frac{\partial^2 E_{y}}{\partial t^2} = \cfrac{1}{ε_{0}\ μ_{0}}\cfrac{\partial^2 E_{y}}{\partial x^2} \label{1-17} \end{equation} 同様に、\eqref{1-13}の両辺の第3成分を\(t\)で微分、\eqref{1-14}の両辺の第2成分を\(x\)で微分すると、それぞれ次式が得られます。 \begin{equation} \require{physics} \pdv{E_{y}}{t}{x} = -μ_{0}\frac{\partial^2 H_{z}}{\partial t^2} \label{1-18} \end{equation} \begin{equation} -\ \frac{\partial^2 H_{z}}{\partial x^2} = ε_{0}\require{physics} \pdv{E_{y}}{x}{t} \label{1-19} \end{equation} これら両式より磁場\(H_{z}\)に関する次式が得られます。 \begin{equation} \frac{\partial^2 H_{z}}{\partial t^2} = \cfrac{1}{ε_{0}\ μ_{0}}\cfrac{\partial^2 H_{z}}{\partial x^2} \label{1-20} \end{equation} \eqref{1-17}、\eqref{1-20}はそれぞれ電場\(\bm{E}\)と磁場\(\bm{H}\)の波動方程式であり、 その伝搬速度は光速cであり、\eqref{1-17}、\eqref{1-20}より、次式で与えられます。 \begin{equation} c = \cfrac{1}{\sqrt{ε_{0}\ μ_{0}\ }} = 3.00\ \x\ 10^8\ \mathrm{m/sec} \label{1-21} \end{equation}
(3)波動方程式の解
次式で表される\(y\)軸方向に振動し\(x\)軸の正方向に進行する電場\(E_{y}\)は、\eqref{1-17}の解となっています
(次式を\eqref{1-17}の両辺に次式を代入することにより確認できます)。
\begin{equation}
E_{y} = E_{0}\sin\ ω(\frac{x}{c}-t) \label{1-22}
\end{equation}
\eqref{1-13}の第3成分の左辺と右辺を入れ替えて\eqref{1-22}を代入すると次式が得られます。
\begin{equation}
\cfrac{\partial H_{z}}{\partial t} = -\frac{ωE_{0}}{μ_{0}c}\cos\ ω(\frac{x}{c}-t) \label{1-23}
\end{equation}
上式を時間\(t\)について積分すると次式が得られます(積分定数を0とします)。
\begin{equation}
H_{z} = H_{0}\sin\ ω(\frac{x}{c}-t) \label{1-24}
\end{equation}
ここで、
\begin{equation}
H_{0} = \frac{E_{0}}{μ_{0}c} \label{1-25}
\end{equation}
\eqref{1-24}で表わされる\(z\)軸方向に振動しx軸正方向に進行する磁場\(H_{z}\)は、\eqref{1-20}の解であることも明らかです。
以上より、電場\(E_{y}\)の波動(電波)と磁場\(H_{z}\)の波動(磁波)は
互いに直交する平面\(x-y\)面、\(x-z\)面内で同時に発生し(両者を合わせて電磁波と呼びます)、\(x\)方向に進行します(図1参照)。
このように、電磁波は、宇宙空間自体が空間的、時間的に変化する電場、磁場(電磁波)を発生し、伝搬する性質を有しており、
発生した電磁波が空間中を光速cで伝搬します。
これにより、電磁波の伝搬のために「エーテル」のような媒体の存在は必要ではないことがわかりました。
なお、電磁波により運ばれるエネルギー密度は次式のポインティングベクトル\(\bm{S}\)で表されます。
\begin{equation}
\bm{S} = \bm{E} \x \bm{H} \label{1-26}
\end{equation}
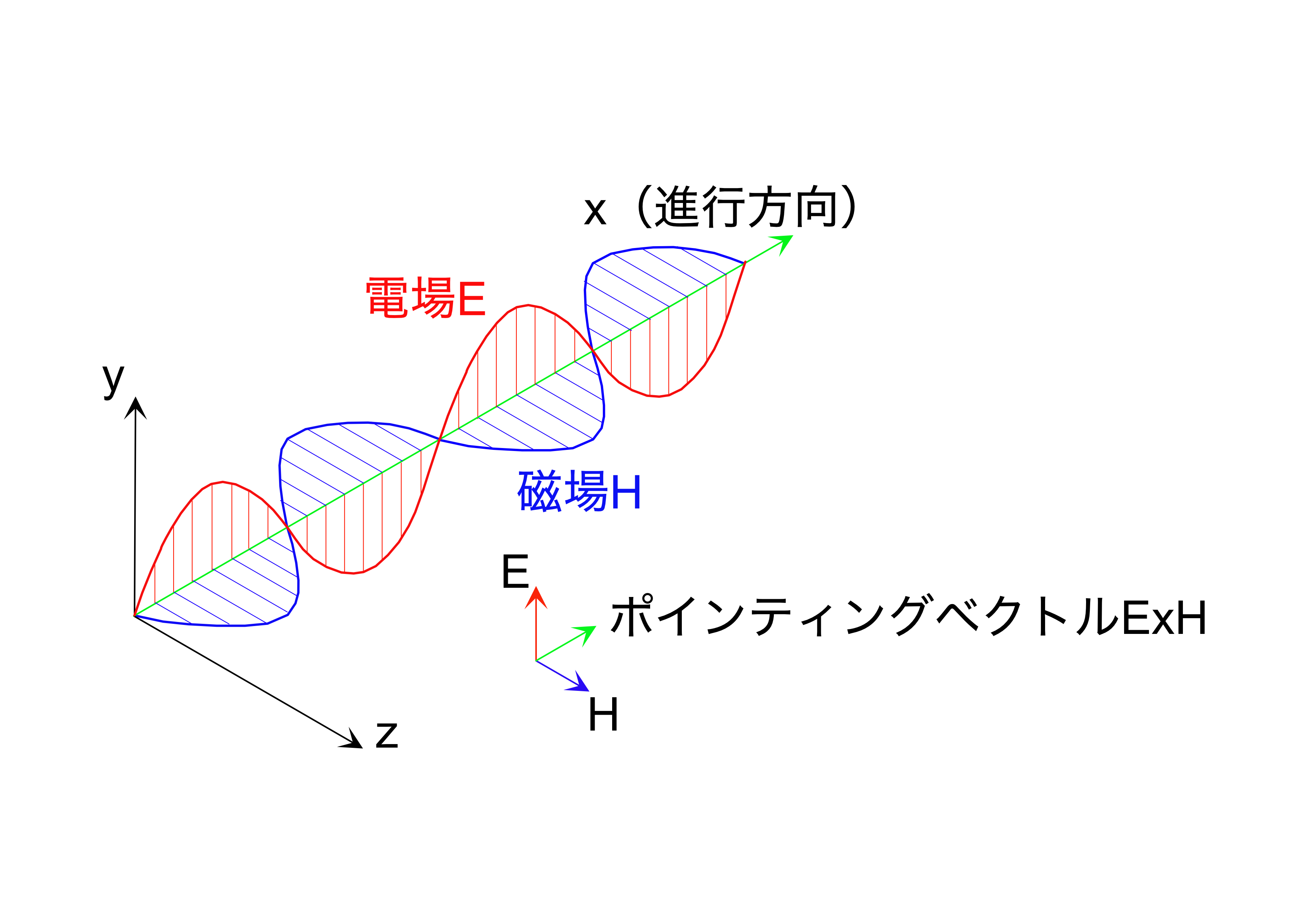
図1 電磁波
以上より、現象論的には下記のことが言えます。
ファラデーの法則\eqref{1-9}と拡張されたアンペールの法則\eqref{1-10}より、磁場の変化と電場の変化とは相互に関係しており、
磁場が変化するとそれに応じて電場が変化し、磁場が変化するとそれに応じて電場が変化することとなります。
したがって、真空空間において磁場(または電場)が変化すると、電場(または磁場)の変化により磁場の波動(「磁波」と呼びます)(波動方程式\eqref{1-20})
(または電場の波動(「電波」と呼びます)(波動方程式\eqref{1-17}))が発生し、
その発生した磁波(または電波)に対応して同時に電波(波動方程式\eqref{1-17})(または磁波(波動方程式\eqref{1-20}))が発生します。
そして、磁場(または電場)の変化に対する発生する電場(または磁場)の方向は、ファラデーの法則\eqref{1-9}(またはアンペールの法則\eqref{1-10})より直交する方向となるため、
磁波と電波の発生する方向は図1に示されるように直交します。
座標変換
物理学の法則を記述するためには座標系が不可欠であるところ、
物理法則はどんな座標系に対しても不変な数学的形式に書かれるはずというのが相対性原理です(【文献】(1))。
物理法則が不変となる座標変換は、従来のニュートン力学においてはガリレー変換であるのに対して
特殊相対性理論においてはローレンツ変換となります。
そこで、ローレンツ変換について、ガリレー変換と対比しつつ説明します。
1.ガリレー変換
物体の運動について取り扱うニュートン力学の基礎となった相対性原理がガリレー(Galilei)の相対性原理です。
ガリレーの相対性原理では「時間はどの観測系でも共通」であるとされています。
したがって、ガリレーの相対性原理では、座標系K(時間\(t\)と三次元空間座標(\(x,y,z\)))
に対して\(x\)方向に速度\(v\)で運動する座標系K'(時間\(t'\)と三次元空間座標(\(x',y',z'\)))
の2つの座標系における質点(物体)の運動の座標と時間の関係は以下のとおりとなります。
下記関係式による座標変換をガリレー変換といいます。
\begin{equation}
\begin{pmatrix}
t'\\
x'\\
y'\\
z'
\end{pmatrix}
=
\begin{pmatrix}
t\\
x-vt\\
y\\
z
\end{pmatrix} \label{2-1}
\end{equation}
2.ローレンツ変換
ニュートン力学に対して、特殊相対性理論では、「光速度不変の原理」により「光速度はどの観測系でも不変(共通)」であるため、
座標系K(時間\(t\)と三次元空間座標(\(x,y,z\)))に対して\(x\)方向に速度\(v\)で運動する座標系(時間\(t'\)と三次元空間座標(\(x',y',z'\)))
の2つの座標系における質点(物体)の運動の座標と時間の関係は以下のとおりとなります。
\begin{equation}
\begin{pmatrix}
t'\\
x'\\
y'\\
z'
\end{pmatrix}
=
\begin{pmatrix}
\cfrac{t-\cfrac{v\ x}{c\ ^{2}}}{\sqrt{1-β\ ^{2}}\ }\\
\cfrac{-vt+x}{\sqrt{1-β\ ^{2}}}\\
y\\
z
\end{pmatrix}
=
\begin{pmatrix}
γ\ (t-\cfrac{β\ x}{c})\\
γ\ (-βct+x)\\
y\\
z
\end{pmatrix} \label{2-2}
\end{equation}
\begin{equation}
β = \cfrac{v}{c}\ \ (\ |β|\lt 1\ ) \label{2-3}
\end{equation}
\begin{equation}
γ = \cfrac{1}{\sqrt{1-β^{2}\ }} \label{2-4}
\end{equation}
上記式による座標変換をローレンツ変換といい、
物理法則がローレンツ変換に対して不変であることを特殊相対性原理といいます。
「特殊」と呼ぶのは、座標変換が任意ではなくローレンツ変換という「特殊」な座標変換に限られるからです。
なお、慣性座標系間の正しい座標変換はローレンツ変換であって、
ガリレー変換は物体の速度\(v\)が光速\(c\)に比べて非常に小さい(\(v\ll c\))特別な場合に成立します
(\eqref{2-2}において、\(\beta \doteqdot 0\ \)とおけば、\eqref{2-2}は\eqref{2-1}に一致します)。
特殊相対性理論では、後記「時空」で説明するように、空間座標(\(x, y, z\))に時間座標tを加えた4次元座標(\(t, x, y, z\))
として取り扱われますが、取り扱いの便宜上、時間軸の次元を空間座標に揃えて一般的に時間軸を\(ct\)とします。
時間軸を\(ct\)とした場合には、\eqref{2-2}に代わって次式を使用します。
\begin{equation}
\begin{pmatrix}
ct'\\
x'\\
y'\\
z'
\end{pmatrix}
=
\begin{pmatrix}
\cfrac{ct-βx}{\sqrt{1-β\ ^{2}}\ }\\
\cfrac{-ut+x}{\sqrt{1-β\ ^{2}}}\\
y\\
z\
\end{pmatrix}
=
\begin{pmatrix}
γ\ (ct) -γβx\\
-γβ\ (ct) + γx\\
y\\
z
\end{pmatrix} \label{2-5}
\end{equation}
上式は次式のように表すことができます。
\begin{equation}
\begin{pmatrix}
ct'\\
x'\\
y'\\
z'
\end{pmatrix}
=
\begin{pmatrix}
\ γ\ & -γβ\ & 0\ & 0\ \\
\ -γβ\ & γ\ & 0\ & 0\ \\
\ 0\ \ & 0\ & 1\ & 0\ \\
\ 0\ \ & 0\ & 0\ & 1\
\end{pmatrix}
\begin{pmatrix}
\ ct\ \\
\ x\ \\
\ y\ \\
\ z\
\end{pmatrix} \label{2-6}
\end{equation}
ここで、次式
\begin{equation}
β = \tanh θ \label{2-7}
\end{equation}
で定義したθを用い、さらに \(γβ = β/\sqrt{1-β^{2}}\) (\eqref{2-3}、\eqref{2-4}参照)を考慮すると次式が得られます。
\begin{equation}
\begin{pmatrix}
\ ct'\ \\
\ x'\ \\
\ y'\ \\
\ z'\
\end{pmatrix}
=
\begin{pmatrix}
\ \cosh θ & -\sinh θ & 0 & 0\ \\
-\sinh θ & \ \cosh θ & 0 & 0\ \\
0 & 0 & 1 & 0\ \\
0 & 0 & 0 & 1\
\end{pmatrix}
\begin{pmatrix}
\ ct\ \\
\ x\ \\
\ y\ \\
\ z\
\end{pmatrix} \label{2-8}
\end{equation}
ここで、\(\sinh θ\)、\(\cosh θ\)、\(\tanh θ\)は、下記により定義される双曲線関数です。
\(\sinh θ = \cfrac{e^{θ}-e^{-θ}}{2} \) \(\sinh θ = \cfrac{e^{θ}+e^{-θ}}{2}\) \(\tanh θ = \cfrac{\tanh θ}{\cosh θ}\)
また、双曲線関数は次の関係式が成立します。
\(\cosh^{2} θ - \sinh^{2} θ = 1\)
\( \cfrac{d}{dθ}\sinh θ = \cosh θ \)
\( \cfrac{d}{dθ}\cosh θ = \sinh θ \)
\( \cfrac{d}{dθ}\tanh θ = 1-\tanh^{2} θ= \sech^{2} θ \)
\eqref{2-8}より、ローレンツ変換は原点を中心とした座標回転の式となることがわかります。
ミンコフスキー時空
従来のニュートン力学の基礎となるガリレーの相対性原理のもとでは、空間(座標)と時間とが関連付けられておらず、
時間は空間座標とは独立して進行する絶対時間であるのに対して、特殊相対性理論のものでは、時間は空間に対して独立ではなく、空間と時間が相互に関連しています。
この特殊相対性理論に基づく現象は、我々の通常経験するものとは異なりますが、時間と空間が一体化したものであり、その結果として、
高速運動する物体の長さが収縮(ローレンツ収縮)したり、時間の経過が遅くなりします。
そこで、相対性理論においては、空間座標(\(x, y, z\))に時間座標ctを加えた4次元座標(\(ct, x, y, z\))として取り扱うこととしています。
このような4次元座標による空間をミンコフスキー時空またはミンコフスキー空間といいます。
このミンコフスキー時空を視覚的に理解できるように便宜上空間座標を2次元(\(x、y\))、
すなわち時空3次元(\(ct、x、y\))として表現したものが図2となります。
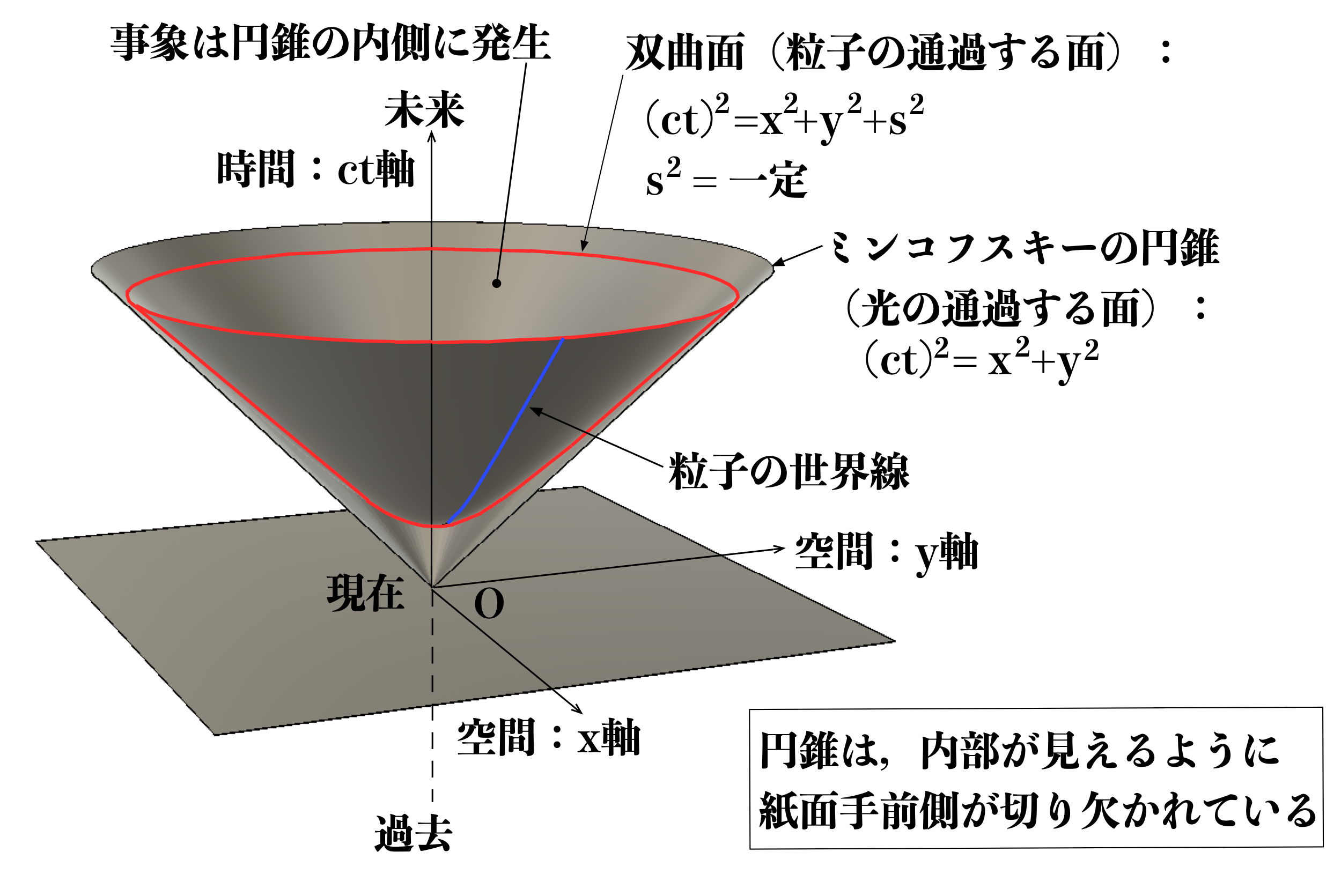
図2 3次元(\(ct, x, y\))のミンコフスキー時空
相対性理論において対象となる出来事を事象といい、事象はミンコフスキー時空においては1つの点として表現し、ミンコフスキー時空における1点は世界点と呼ばれます。
質点の運動はミンコフスキー時空では一般に曲線として表現され、それを世界線と呼びます。
2つの世界点(\(ct_{1},x_{1},y_{1},z_{1}\))と(\(ct_{2},x_{2},y_{2},z_{2}\))の間の量\({s_{12}}^{2}\)を
\begin{equation}
{s_{12}}^{2} = -(ct_{2}-ct_{1})^{2} + (x_{2}-x_{1})^{2} + (y_{2}-y_{1})^{2} + (z_{2}-z_{1})^{2} \label{3-1}
\end{equation}
で定義したとき、\(s_{12}\)を世界間隔と呼びます。
世界間隔は空間座標の3次元空間における距離をミンコフスキー時空に拡大したものです。
したがって、ミンコフスキー時空の2つの世界点(\(ct,x,y,z\))と(\(ct+d(ct),\ x+dx,\ y+dy,\ z+dz\))の間の世界間隔は次式により求まる\(ds\)となります。
\begin{equation}
ds^{2} = -(cdt)^{2} + dx^{2} + dy^{2} + dz^{2} \label{3-2}
\end{equation}
K座標系の点P(\(ct, x, y, z\))を座標変換したK'座標系のP'(\(ct', x', y', z'\))について下記式により定義された\(s^{2}\)、\(s’^{2}\) は、
ローレンツ変換の式を用いると
\begin{equation}
s^{2}=-(c\ t)^{2}+x^{2}+y^{2}+z^{2}= -(c\ t'\ )^{2}+x'\ ^{2}+y'\ ^{2}+z'\ ^{2}=s'\ ^{2} = \mathrm{Const(一定)} \label{3-3}
\end{equation}
となり、異なる観測系(時空)において\(s^{2}\)が一定となります。
\(s, s'\)は、3次元空間におけるそれぞれの座標の原点から点P、P'までの距離の相当するものであり、「世界長さ」と呼ばれています。
ミンコフスキー時空の空間座標を2次元の平面(\(xーy\)座標)に垂直な方向を時間軸(\(ct\)軸)とする3次元座標系(\(ct, x, y\))で考えると、
\begin{equation}
-(c\ t)^{2}+x^{2}+y^{2} = \mathrm{Const(一定)} \label{3-4}
\end{equation}
の表す曲面は双曲面(二葉回転双曲面)となります(図2参照)。
ミンコフスキー時空では、原点を通過する光は次式で表される円錐(原点を通り時間軸から45度傾いた円錐であり、ミンコフスキー円錐といいます。)の上を通過することになります。
そこで、ミンコフスキー円錐を光円錐ともいいます。
\begin{equation}
-(c\ t)^{2}+x^{2}+y^{2}+z^{2} = 0 \label{3-5}
\end{equation}
ミンコフスキー時空で発生する事象の範囲は\eqref{3-4}を満たす座標(\(ct, x, y, z\))の集合となるため、ミンコフスキー円錐の内側となります(図2参照)。
時空図
ミンコフスキー時空は、正確には4次元(時間座標が1次元、空間座標が3次元)ですが、静止座標系Kと移動座標系K’を取り扱う場合は、
移動座標系K'の運動方向を静止座標系Kの\(x\)方向として処理することにより、空間座標については静止座標Kの\(x\)座標のみとして処理することが可能です。
したがって、通常、ミンコフスキー時空を図3のような2次元(\(ct, x\))として表現、検討することができるため(文献(2))、
有用です。
そこで、時空図について簡単に説明します。
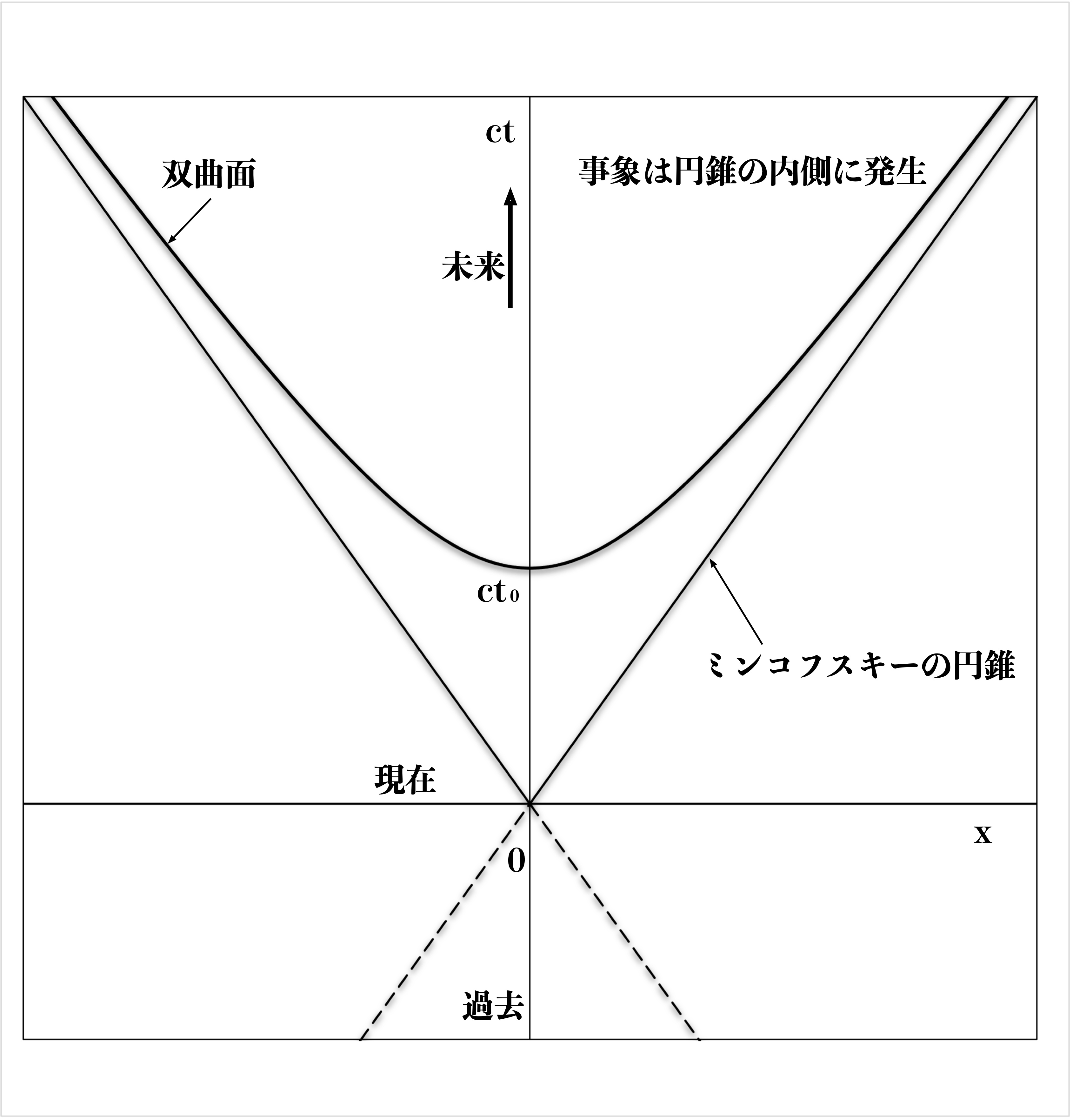
図3 時空図
1.基本時空図
慣性系K(\(ct, x\))に対して\(x\)軸方向に速度\(v\)で相対運動する慣性系K'(\(ct', x'\))について、
慣性系Kを静止しているとした時空図は図4のように表されます。
静止している慣性系Kでは時間(座標)\(ct\)が \(x=0\) の状態で鉛直上方に向かって直線的に増加するのに対して、
運動している慣性系K'では時間(座標)\(ct'\)は傾き\(c/v\)(\(=1/β\))の直線、および空間座標\(x'\)は傾き\(v/c\)(=β)の直線に乗って増加します。
光は傾き1の直線により増加し、慣性系K'の相対速度\(v\)が増加すると\(ct'\)の直線の傾きが小さくなるとともに\(x'\)の傾きが大きくなり、
光の傾きに近づいていきます。
なお、慣性系K'は慣性系Kをローレンツ変換したものですが、幾何学的には慣性系K'の座標軸は
(構成する座標軸が直交しない)斜交座標となります。
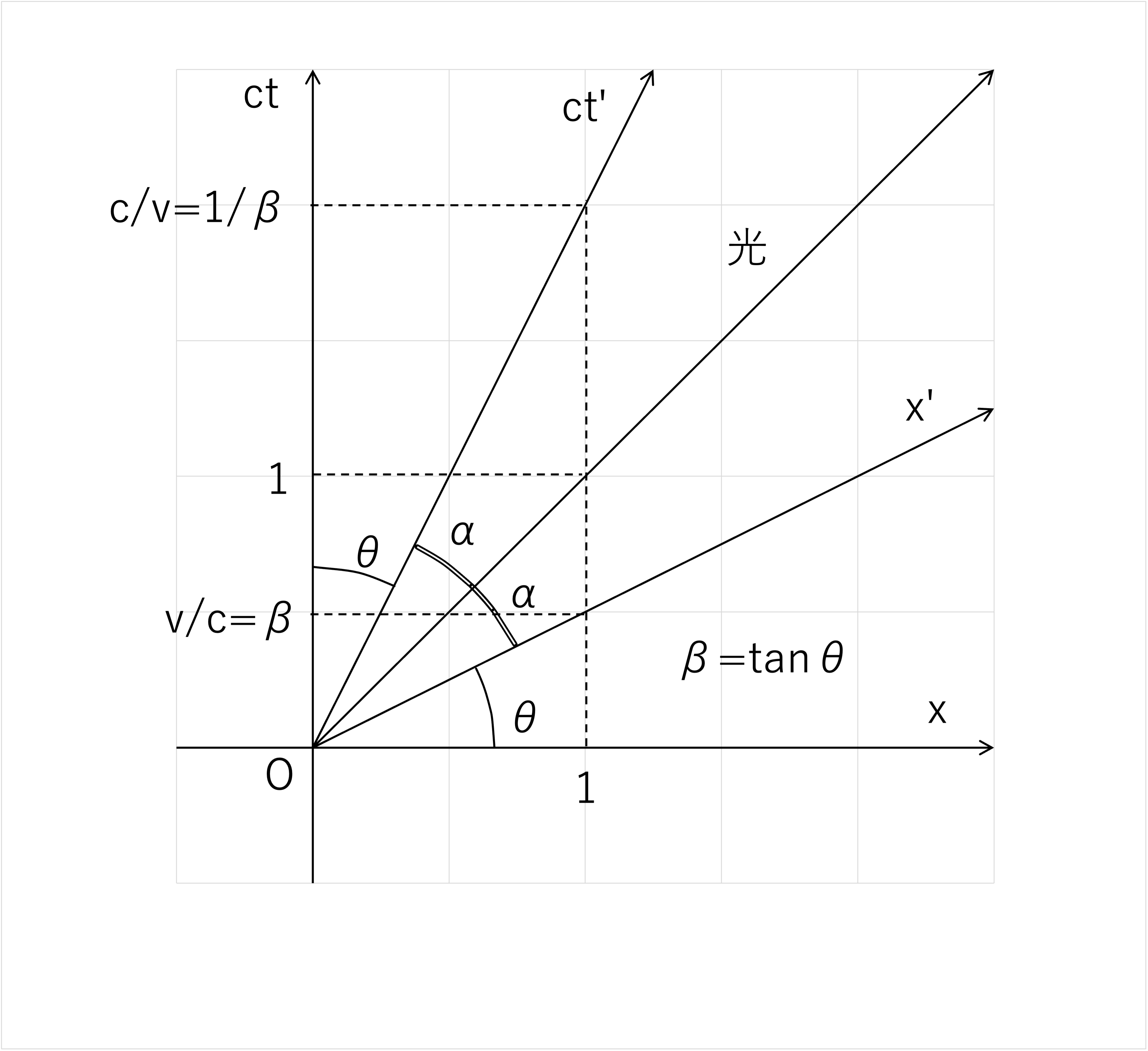
図4 基本時空図
2.運動物体内の時間の遅れの時空図
運動物体内の時間の遅れを時空図で表示することについて説明します。
静止する座標系K(\(ct, x\))に対して速度\(v=βc\)(\(0\leqq β\lt 1\))で運動するを座標系K'(\(ct', x'\))について、
それぞれの座標系から観測した場合の相手の座標系の時間を遅れを表示する時空図が図5です。
図5では、出発時の2つの座標系の時刻を\(ct=ct'=0\)(光年)に合わせて座標系K'を座標系Kの\(x\)軸方向に速度\(v\)で運動を開始し、
座標系K'が距離\(b\)(光年)に到達した時点でそれぞれの座標系から相手の座標系固定の経過時間(時刻)を観測します。
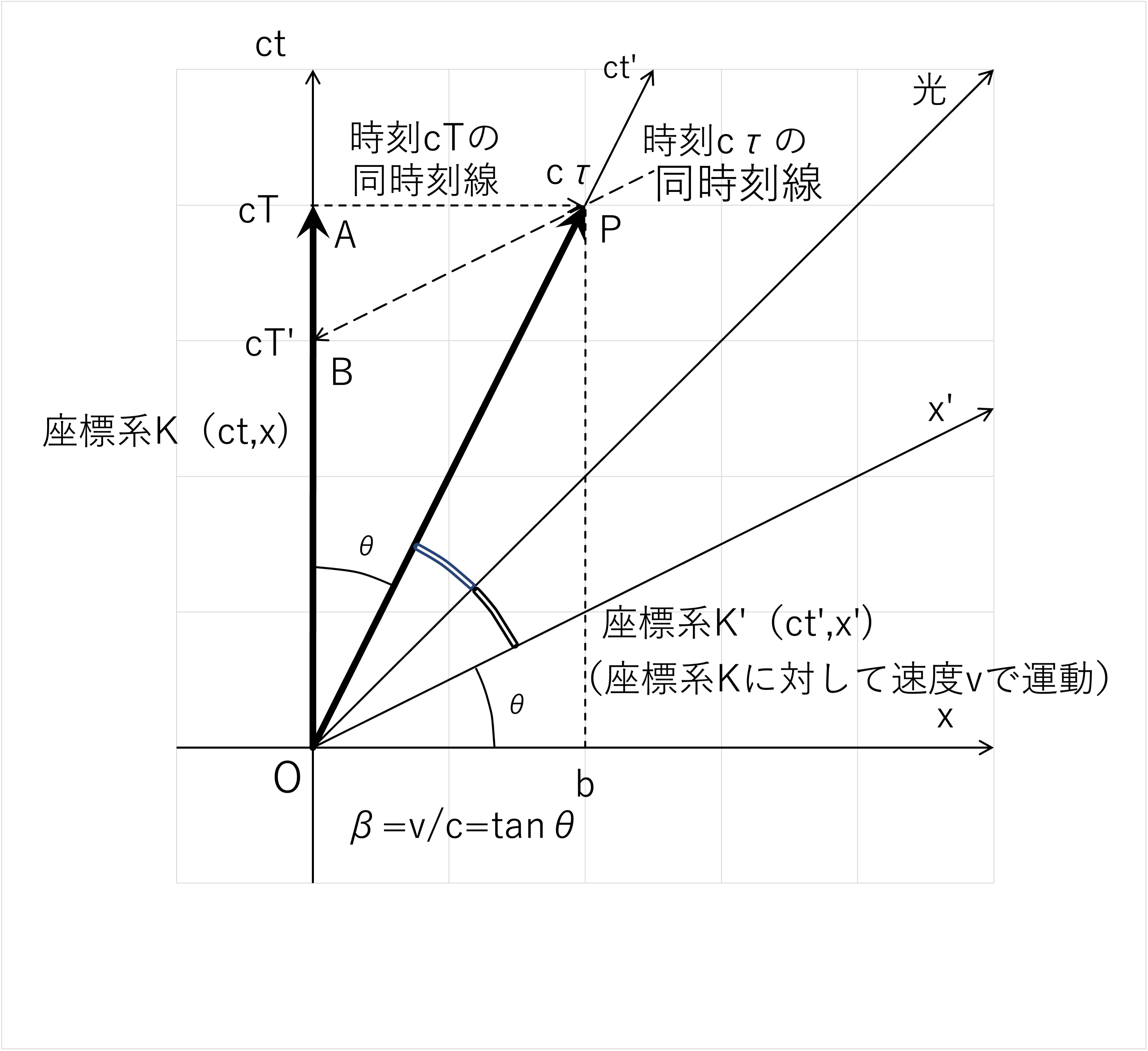
図5 運動物体内の時間の遅れの時空図
(1) 座標系Kから観測した座標系K'固定時計の時間遅れ
座標系Kにおける世界点Aの同時刻は世界点Aを通りx軸に平行な直線上の世界点(の集合)となります。このため、座標系Kから座標系K'を観測したときに
(座標系Kの)世界点Aと同時刻にある(座標系K'の)世界点はPとなります。
したがって、座標系Kから座標系K'を観測したときの座標系K'固定時計の時刻は\(cτ\)であり、τは本文ページの(6)式において
\(T\)をτに置換した次式により求まります。
\(τ=t\sqrt{1-β^{2}}\)
なお、\eqref{2-3}より、0\(\lt\sqrt{1-β^{2}}\leqq1\)
(2) 座標系K'から観測した座標系K固定時計の時間遅れ
上記と逆に座標系K'が静止し、座標系Kが運動している場合となります。
座標系K'における世界点Pの同時刻は世界点Pを通り\(x'\)軸に平行な直線上の世界点(の集合)となります。
このため、座標系K'から座標系Kを観測したときに(座標系K'の)世界点Pと同時刻にある(座標系Kの)世界点はBとなります。
したがって、座標系K'から座標系Kを観測したときの座標系K固定時計の時刻は\(cT'\)となります。
ここで、本文ページの(6)式において\(T\)は静止座標系固定時計の時間、\(t\)は運動座標系固定時計の時間であるため、\(T'\)は、本文ページの(6)式において
\(T\)、\(t\)をそれぞれ\(T'\)、τに置き換えた下記式に求まります。
\(T'=τ\sqrt{1-β^{2}}\)
3.本文ページ例題3の時空図
列車座標系K'(\(ct', x'\))を基準(静止)座標系、地面座標系K(\(ct, x\))を相対運動系として描いた時空図が図6です。
各座標系の時間座標軸\(ct\)又は\(ct'\)の各時刻に対して空間座標軸\(x'\)又は\(x\)に平行な直線上にある事象がそれぞれの座標系の同時刻に発生したものとなります。
なお、この時空図は列車座標系K'を基準座標系として描いており、地面座標系Kは列車座標系K'に対して速度\(-v\)で運動しているため、
列車座標軸K'の時間座標軸\(ct'\)、空間座標軸\(x'\)に対する地面座標系Kの時間座標軸\(ct\)、
空間座標軸\(x\)の直線の傾きの方向が前記「基本的時空図」とは逆になっています。
列車座標系K'では先端Aと後端Bに対応する事象Fと事象Rは時間座標軸\(ct'\)の時刻\(ct'0\)に発生していることがわかります。
これに対して、地面座標系Kでは後端Bに対応する事象Rは時間軸\(ct\)の\(ct1\)に発生し、
先端Aに対応する事象Fは時間軸\(ct\)の\(ct2\)に発生しており、時間的には\(ct1\)が\(ct2\)より前になります。
したがって、地面座標系Kにおいて、ビーム光は先端より後端の方に先に到着しており、同時ではないことが観測されることがわかります。
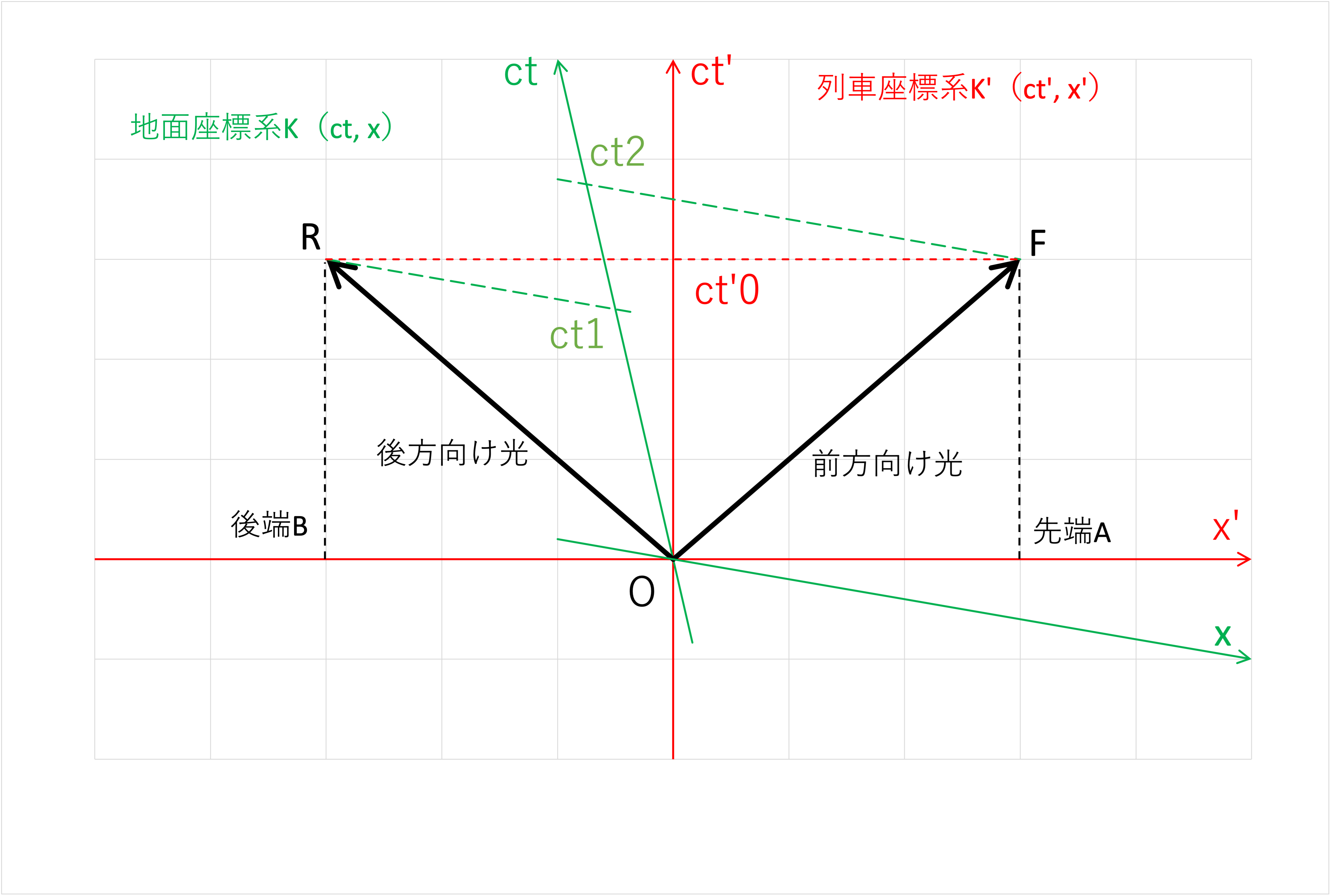
図6 本文ページ例題3の時空図
物理法則の共変形式
慣性座標系Kから別の慣性座標系K’に座標変換するとき、
その座標変換に対して物理法則が不変であることが自明な数学的形式を「共変形式」と呼びます。
以下、代表的な物理法則についてローレンツ変換に対する共変形式を紹介します。
1.数学的準備
(1)座標表示
時空点の座標として、\(t,x,y,z\)の代わりに、
\(x^{i} = (x^{0},x^{1},x^{2},x^{3}) = (ct,x,y,z)\)
と表わすこととします。\(i\)は0,1,2,3の値を取る添字であり、\(i\)に特定の値を入れたときは座標の特定の成分を表すものとします
(例えば、\(x^{3}=z\))。
\(x^{i}\)のように4次元座標\(x^{i} = (x^{0},x^{1},x^{2},x^{3}) = (ct,x,y,z)\)に対応する4成分を持つベクトルを
「4元ベクトル」と呼びます。4次元空間の位置ベクトル\(x^{i}\)は4元ベクトルの一例です。
(2)座標変換とテンソル
①テンソルの定義及び表記方法
相対性理論を理解、解析する上で「テンソル」は非常に重要なものとなります。そこで、先ずテンソルについて説明します。
「テンソル」とは、ベクトルを別のベクトルに変換する線形作用素をいいます。
4次元ベクトル\(\bm p\)(\(p^{0},\ p^{1},\ p^{2},\ p^{3}\))、
4次元ベクトル\(\bm q\)(\(q_{0},\ q_{1},\ q_{2},\ q_{3}\))、
テンソル\(T\)として、ベクトル\(\bm p\)をベクトル\(\bm q\)への変換を行列形式で表すと次式となります。
\begin{equation}
\begin{pmatrix}
\ q_{0}\ \\
\ q_{1}\ \\
\ q_{2}\ \\
\ q_{3}\
\end{pmatrix}
=
\begin{pmatrix}
T_{00} & T_{01} & T_{02} & T_{03}\\
T_{10} & T_{11} & T_{12} & T_{13}\\
T_{20} & T_{21} & T_{22} & T_{23}\\
T_{30} & T_{31} & T_{32} & T_{33}
\end{pmatrix}
\begin{pmatrix}
\ p^{0}\ \\
\ p^{1}\ \\
\ p^{2}\ \\
\ p^{3}\
\end{pmatrix} \label{5-1}
\end{equation}
上式のような行列形式で表記するのは煩わしいので、次式のように表記することとします。
\begin{equation}
q^{i} = \sum_{j=0}^{3}{T^{i}}_{j}\ p^{j}\qquad (i=0,1,2,3) \label{5-2}
\end{equation}
さらに、上式の和記号\(\sum\)を省略して次式のように簡略して表記することとします(この省略を「アインシュタインの省略」と呼びます)。
\begin{equation}
q^{i} = {T^{i}}_{j}\ x^{j} \label{5-3}
\end{equation}
②ローレンツ変換のテンソル表記
ミンコフスキー時空の座標\(x^{i} = (x^{0},x^{1},x^{2},x^{3}) = (ct,x,y,z)\)においてローレンツ変換は\eqref{2-6}よりテンソルとなるので、ローレンツ変換をテンソル形式で表せば次式となります。
\begin{equation}
\bm x' = \bm L \bm x \label{5-4}
\end{equation}
ここで、\(\bm L\)は次式で表されるローレンツ変換行列です。
\begin{equation}
\bm L =
\begin{pmatrix}
\ {L^{0}}_{0}\ & {L^{0}}_{1}\ & {L^{0}}_{2}\ & {L^{0}}_{3}\ \\
\ {L^{1}}_{0}\ & {L^{1}}_{1}\ & {L^{1}}_{2}\ & {L^{1}}_{3}\ \\
\ {L^{2}}_{0}\ & {L^{2}}_{1}\ & {L^{2}}_{2}\ & {L^{2}}_{3}\ \\
\ {L^{3}}_{0}\ & {L^{3}}_{1}\ & {L^{3}}_{2}\ & {L^{3}}_{3}\
\end{pmatrix}
\equiv
\begin{pmatrix}
\ γ\ & -γβ\ & 0\ & 0\ \\
\ -γβ\ & γ\ & 0\ & 0\ \\
\ 0\ \ & 0\ & 1\ & 0\ \\
\ 0\ \ & 0\ & 0\ & 1\
\end{pmatrix} \label{5-5}
\end{equation}
アインシュタインの省略をすれば次式のように表記されます。
\begin{equation}
x'^{i} = {L^{i}}_{j}\ x^{j} \label{5-6}
\end{equation}
(3)スカラー
ローレンツ変換\eqref{5-6}は1次変換であり、次式で表すことができます。
\begin{equation}
x'^{i} = \dd{x'^{i}}{x^{j}}x^{j} \label{5-9}
\end{equation}
したがって、\({L^{i}}_{j}\)は次式で表すことができます。
\begin{equation}
{L^{i}}_{j} = \dd{x'^{i}}{x^{j}} \label{5-10}
\end{equation}
\(x\)座標系の点\(x\)で定義された物理量\(\phi(x)\)がローレンツ変換により\(x'\)系に移ったとき、
\(x'\)系での物理量\(\phi'(x')\)の値が元のx系での物理量\(\phi(x)\)に等しい場合、
この物理量を「スカラー」といいます。
\begin{equation}
\phi'(x') = \phi(x) \label{5-11}
\end{equation}
ミンコフスキー時空における世界間隔\(ds\)の2乗\(ds^{2}\)(\eqref{3-2}で前述)
\begin{equation}
ds^{2} = η_{ij}x^{i}x^{j} \label{5-12}
\end{equation}
\begin{equation}
η_{ij} =
\begin{pmatrix}
-1\ & 0\ & 0\ & 0 \\
0\ & 1\ & 0\ & 0 \\
0\ & 0\ & 1\ & 0 \\
0\ & 0\ & 0\ & 1
\end{pmatrix} \label{5-13}
\end{equation}
がスカラーであることを以下に説明します。
なお、\(η_{ij}\)をミンコフスキー時空の計量テンソルといいます。
\(ds'^{2}\)は、\eqref{5-10}を考慮すると、
\begin{align}
ds'^{2} &= η_{ij}x'^{i}x'^{j} = η_{ij}({L^{i}}_{j}x^{j})({L^{j}}_{i}x^{i}) = η_{ij}(\dd{x'^{i}}{x^{j}}x^{j})(\dd{x'^{j}}{x^{i}}x^{i}) \\ \notag
&= η_{ij}x^{j}x^{i} \\ \notag
&= ds^{2} \label{5-14}
\end{align}
となり、\(ds^{2}\)はローレンツ変換に対して値が変化しないため、スカラーとなります。
また、世界間隔から定義される固有時間
\begin{equation}
dτ = \cfrac{\ 1\ }{c}\sqrt{-ds^{2}} \label{5-15}
\end{equation}
もスカラーです。
(4)反変ベクトルと共変ベクトル
①反変ベクトル
\(x\)座標系において4成分を持つベクトル\(U^{i}(x)=(U^{0}(x),U^{1}(x),U^{2}(x),U^{3}(x))\)を
\(x'\)系へ座標変換するときに次式のように変換される性質をもつ場合に、
このベクトルを反変ベクトルといいます。
反変ベクトルであることを示すためにそのベクトルの右上に添字を書くこととしています。
\begin{equation}
U'^{i}(x') = \dd{x'^{i}}{x^{j}}U^{j}(x) \label{5-16}
\end{equation}
したがって、\eqref{5-10}より、\(\cfrac{\partial x'^{i}}{\partial x^{j}} = {L^{i}}_{j}\)であるため、ローレンツ変換によって変換されるベクトルは反変ベクトルとなります。
②共変ベクトル
\(x\)座標系において4成分を持つベクトル\(V_{i}(x)=(V_{0}(x),V_{1}(x),V_{2}(x),V_{3}(x))\)を
\(x'\)系へ座標変換するときに、
ローレンツ変換行列\({L^{i}}_{j}\)の逆行列\({(L^{-1})^{i}}_{j}\)を使用して次式により変換される場合に、
このベクトルを共変ベクトルといいます。共変ベクトルであることを示すためにそのベクトルの右下に添字を書くこととしています。
\begin{equation}
V'_{j}(x') = {(L^{-1})^{i}}_{j}\ V_{i}(x) \label{5-17}
\end{equation}
ここで、
\begin{equation}
{(L^{-1})^{i}}_{j} = \dd{x^{i}}{x'^{j}} \label{5-18}
\end{equation}
\begin{equation}
\bm L^{-1} =
\begin{pmatrix}
\ {(L^{-1})^{0}}_{0}\ & {(L^{-1})^{0}}_{1}\ & {(L^{-1})^{0}}_{2}\ & {(L^{-1})^{0}}_{3}\ \\
\ {(L^{-1})^{1}}_{0}\ & {(L^{-1})^{1}}_{1}\ & {(L^{-1})^{1}}_{2}\ & {(L^{-1})^{1}}_{3}\ \\
\ {(L^{-1})^{2}}_{0}\ & {(L^{-1})^{2}}_{1}\ & {(L^{-1})^{2}}_{2}\ & {(L^{-1})^{2}}_{3}\ \\
\ {(L^{-1})^{3}}_{0}\ & {(L^{-1})^{3}}_{1}\ & {(L^{-1})^{3}}_{2}\ & {(L^{-1})^{3}}_{3}\
\end{pmatrix}
=
\begin{pmatrix}
\ γ\ & γβ\ & 0\ & 0\ \\
\ γβ\ & γ\ & 0\ & 0\ \\
\ 0\ \ & 0\ & 1\ & 0\ \\
\ 0\ \ & 0\ & 0\ & 1\
\end{pmatrix} \label{5-19}
\end{equation}
\(\bm L^{-1}\)はローレンツ変換行列\(\bm L\)の逆行列であるため、ローレンツ変換を表す\eqref{2-2}、\eqref{2-3}の成分中の速度\(v\)を\(-v\)に置換し、その結果、
逆行列の成分\({(L^{-1})^{i}}_{j}\)はローレンツ変換行列の定義式である\eqref{5-6}の成分\({L^{i}}_{j}\)中の\(β\)を\(-β\)に置換したものとなります。
(5)反変テンソル、共変テンソル、混合テンソル
①反変テンソル
2つの反変ベクトル\(A^{i}(x)\)、\(B^{j}(x)\)の成分の積\(A^{i}B^{j}\)がその\(i,j\)成分となっているテンソル\(T^{ij}(x)\)を2階のテンソルといいます。
\begin{equation}
T^{ij}(x) = A^{i}(x)\cdot B^{j}(x) =
\begin{pmatrix}
A^{0}B^{0} & A^{0}B^{1} & A^{0}B^{2} & A^{0}B^{3} \\
A^{1}B^{0} & A^{1}B^{1} & A^{1}B^{2} & A^{1}B^{3} \\
A^{2}B^{0} & A^{2}B^{1} & A^{2}B^{2} & A^{2}B^{3} \\
A^{3}B^{0} & A^{3}B^{1} & A^{3}B^{2} & A^{3}B^{3} \\
\end{pmatrix} \label{5-20-1}
\end{equation}
上式により表されるテンソル\(T^{ij}(x)\)は、座標変換により次式のように変換することができるため、
2階の反変テンソルと呼ばれます。
\begin{equation}
T'^{ij}(x') = \dd{x'^{i}}{x^{k}}\dd{x'^{j}}{x^{l}}T^{kl}(x) = {L^{i}}_{k}{L^{j}}_{l}T^{kl}(x) \label{5-20-2}
\end{equation}
②共変テンソル
2階の反変テンソルと同様に、2つの共変ベクトル\(A_{i}(x)\)、\(B_{j}(x)\)の成分の積\(A_{i}B_{j}\)がその成分\(i,j\)成分となっている2階のテンソル
\begin{equation}
T_{ij}(x) = A_{i}(x)\cdot B_{j}(x) \label{5-20-3}
\end{equation}
は、座標変換により次式のように変換することができるため、2階の共変テンソルと呼ばれます。
\begin{equation}
T'_{ij}(x') = \dd{x^{k}}{x'^{i}}\dd{x^{l}}{x'^{j}}T_{kl}(x) = {(L^{-1})^{k}}_{i}{(L^{-1})^{l}}_{j}T_{kl}(x) \label{5-20-4}
\end{equation}
③混合テンソル
上記と同様に、1つの共変ベクトル\(A^{i}(x)\)と1つの共変ベクトル\(B_{j}(x)\)の成分の積がその成分\(i,j\)成分となっている次式により表される2階のテンソル
\begin{equation}
T^{i}_{j}(x) = A^{i}(x)\cdot B_{j}(x) \label{5-20-5}
\end{equation}
は、座標変換により次式のように変換することができるため、2階の混合テンソルと呼ばれます。
\begin{equation}
{T'^{i}}_{j}(x') = \dd{x'^{i}}{x^{k}}\dd{x^{l}}{x'^{j}}{T^{k}}_{l}(x) = {L^{i}}_{k}{(L^{-1})^{l}}_{j}{T^{k}}_{l}(x) \label{5-20-6}
\end{equation}
2.電磁場方程式
4つの電磁場方程式\eqref{1-7}〜\eqref{1-10}からテンソル式を作成してみます。
先ず、4つの電磁場方程式うち、\eqref{1-4}と\eqref{1-5}からテンソル式を作成してみます。
\eqref{1-4}より次式が得られます。
\begin{equation}
0 - c\partial_{1}B_{x} - c\partial_{2}B_{y} - c\partial_{3}B_{z} = 0 \label{5-21}
\end{equation}
同様に、\eqref{1-5}より次式が得られます。
\begin{equation}
\begin{matrix}
c\partial_{0}B_{x} + 0 + \partial_{2}E_{z} - \partial_{3}E_{y} = 0 \\
c\partial_{0}B_{y} - \partial_{1}E_{z} + 0 - \partial_{3}E_{x} = 0 \\
c\partial_{0}B_{z} + \partial_{1}E_{y} - \partial_{2}E_{x} + 0 = 0
\end{matrix} \label{5-22}
\end{equation}
ここで、\(\partial_{i}\)は偏微分\(\partial/\partial{x^{i}}\)を表わす記号(\(\partial_{i}=\partial / \partial x^{i}\))(\(i=0,1,2,3\))です。
電磁場のテンソル\(f_{ij}\)を
\begin{equation}
f_{ij} =
\begin{pmatrix}
0\ & -\cfrac{1}{c}E_{x}\ & -\cfrac{1}{c}E_{y}\ & -\cfrac{1}{c}E_{z} \\
\cfrac{1}{c}E_{x}\ & 0\ & B_{z}\ & -B_{y} \\
\cfrac{1}{c}E_{y}\ & -B_{z}\ & 0\ & B_{x} \\
\cfrac{1}{c}E_{z}\ & B_{y}\ & -B_{x}\ & 0
\end{pmatrix} \label{5-23}
\end{equation}
と定義すると、\eqref{5-21}から次式が得られます。
\begin{equation}
\partial_{1}f_{32} + \partial_{2}f_{13} + \partial_{3}f_{21} = 0 \label{5-24}
\end{equation}
同様に、\eqref{5-22}から次式が得られます。
\begin{equation}
\begin{matrix}
\partial_{0}f_{23} + \partial_{2}f_{30} + \partial_{3}f_{02} = 0 \\
\partial_{0}f_{31} + \partial_{1}f_{03} + \partial_{3}f_{10} = 0 \\
\partial_{0}f_{12} + \partial_{1}f_{20} + \partial_{2}f_{01} = 0
\end{matrix} \label{5-25}
\end{equation}
\eqref{5-24}、\eqref{5-25}を簡単なテンソル式としてまとめると次式が得られます。
\begin{equation}
\partial_{i}f_{jk} + \partial_{j}f_{ki} + \partial_{k}f_{ij} = 0\quad (i,j,k=0,1,2,3) \label{5-26}
\end{equation}
ここで、\(i,j,k\)はそれぞれ4つの数の組み合わせであるため、\(4\times 3\times 2=24\)個の式となるが、
多くは恒等式や独立でない式であるため、独立式は\eqref{1-4}、\eqref{1-5}に対応する\eqref{5-24}、\eqref{5-25}の4つです。
次に、4つの電磁場方程式の残りの2つの\eqref{1-3}および\eqref{1-6}からテンソル式を作成してみます。
\eqref{1-3}から次式が得られます。
\begin{equation}
0 + c\partial_{1}D_{x} + c\partial_{2}D_{y} + c\partial_{3}D_{z} = cρ \label{5-27}
\end{equation}
同様に、\eqref{1-6}より次式が得られます。
\begin{equation}
\begin{matrix}
-c\partial_{0}D_{x} + 0 + \partial_{2}H_{z} - \partial_{3}H_{y} = j_{x} \\
-c\partial_{0}D_{y} - \partial_{1}H_{z} + 0 - \partial_{3}H_{x} = j_{y} \\
-c\partial_{0}D_{z} + \partial_{1}H_{y} - \partial_{2}H_{x} + 0 = j_{z}
\end{matrix} \label{5-28}
\end{equation}
ここで、電荷密度ρ、電流密度ベクトル\((j_{x},j_{y},j_{z})^{T}\)から、4元電流密度\(\bm j^{i}\)を次式のように定義します。
\begin{equation}
\bm j^{i} = (cρ,j_{x},j_{y},j_{z})^T \label{5-29}
\end{equation}
電磁場のテンソル\(f_{ij}\)を反変テンソルとして表現した次式
\begin{equation}
f^{ik} = η^{ij}η^{kl}f_{jl} =
\begin{pmatrix}
0\ & \cfrac{1}{c}E_{x}\ & \cfrac{1}{c}E_{y}\ & \cfrac{1}{c}E_{z} \\
-\cfrac{1}{c}E_{x}\ & 0\ & B_{z}\ & -B_{y} \\
-\cfrac{1}{c}E_{y}\ & -B_{z}\ & 0\ & B_{x} \\
-\cfrac{1}{c}E_{z}\ & B_{y}\ & -B_{x}\ & 0
\end{pmatrix} \label{5-30}
\end{equation}
および\eqref{1-1}(\(\bm D=ε_{0}\bm E\))、\eqref{1-21}(\(c^{2}=1/ε_{0}μ_{0}\))を使用して
\eqref{5-27}乃至\eqref{5-29}をまとめると次式が得られます。
\begin{equation}
\dd{f^{ik}}{x^{k}} = μ_{0}\bm j^{i} \label{5-31}
\end{equation}
\eqref{5-26}は3階のテンソル方程式、\eqref{5-31}はベクトル方程式であるため、
ローレンツ変換により他の座標系に変換されてもその座標系でも方程式の形は同一となります
3.質点の運動方程式
質点の質量を\(m\)、座標を\(\bm{x}\)として次式で表されるニュートンの運動方程式は、
\eqref{2-6}から、ローレンツ変換に対して時間\(t\)は変化するのでスカラーではありません。
\begin{equation}
m\cfrac{d^{2}\bm{x}}{dt^{2}} = \bm{f} \label{5-32}
\end{equation}
このため、速度\(\cfrac{dx}{dt}\)もベクトルとはならないため、
\eqref{5-32}により表されたものはローレンツ変換に対して共変形式とはなっていません。
一方、質点に固定した座標系における時間である固有時間τはローレンツ変換に対して変化しないスカラー量です。
そこで、固有時間τを利用して共変形式の運動方程式を導出することとします。
(1)4元速度
運動する質点の4元速度を次式で定義します。
\begin{equation}
u^{i} = \frac{dx^{i}(τ)}{dτ} \label{5-33}
\end{equation}
\(dx^{i}\)は反変ベクトル、\(dτ\)がスカラーであるため、
\(u^{i}\)は通常の速度\(\cfrac{dx}{dt}\)に対応しており、反変ベクトルとして次式が得られます。
\begin{equation}
u'^{i} = \frac{dx'^{i}}{dτ'} = \cfrac{{L^{i}}_{j}\ x^{j}(τ)}{dτ}
= {L^{i}}_{j}\cfrac{dx^{j}(τ)}{dτ} = {L^{i}}_{j}\ u^{j} \label{5-34}
\end{equation}
ここで、固有時間τと座標時間\(t\)との関係は次式のように表されます。
\begin{equation}
dτ = \sqrt{1-\cfrac{1}{c^{2}}\biggl(\cfrac{dx(t)}{dt}\biggr)^{2}}\ dt = \sqrt{1-β^{2}}\ dt = \cfrac{\ 1\ }{γ}dt \label{5-35}
\end{equation}
したがって、\(u^{i}\)の成分は次式により表されます。
\begin{align}
u^{i} &= \cfrac{dx^{i}(τ)}{dτ} = γ\cfrac{dx^{i}(τ)}{dt} \notag \\
&= γ\biggl(\cfrac{d(ct)}{dt},\ \cfrac{dx^{1}(t)}{dt},\ \cfrac{dx^{2}(t)}{dt},\ \cfrac{dx^{3}(t)}{dt}\biggr) \notag \\
&= γ\biggl(c,\ \cfrac{dx^{1}(t)}{dt},\ \cfrac{dx^{2}(t)}{dt},\ \cfrac{dx^{3}(t)}{dt}\biggr) \label{5-36}
\end{align}
\eqref{5-36}より、質点の速度\(\cfrac{dx^{i}}{dt}\ (i=1,2,3)\)が \(c\) に比べて非常に小さいとき(\(|β|\ll c,\ γ\simeq 1\))、
\(u^{i}\)の空間成分\(\ γ\cfrac{dx^{i}}{dt}\ \)は非相対論としての速度となります。
4元速度の2乗\(u^{i}u_{i}\)は、\eqref{5-12}を利用すると
\begin{equation}
u^{i}u_{i} = η_{ij}u^{i}u^{j} = η_{ij}\cfrac{dx^{i}}{dτ}\cfrac{dx^{j}}{dτ}
= \biggl(\cfrac{ds}{dτ}\biggr)^{2} = -c^{2} \label{5-37}
\end{equation}
であり、常に一定(\(-c^{2}\))となります。
4元速度\(u^{i}\)は4成分から成りますが、上式により、独立な成分は3成分のみとなります。
(2)4元運動量とエネルギー
4元運動量を
\begin{equation}
p^{i} = mu^{i} \label{5-38}
\end{equation}
と定義すると、4元運動量の2乗は
\begin{equation}
p^{i}p_{i} = m_{0}^{2}u^{i}u_{i} = -m_{0}^{2}c^{2} \label{5-39}
\end{equation}
となり、常に一定となります。
このため、4元運動量も4成分からなりますが、独立成分は3成分のみとなります。
ここで、エネルギー\(E\)を
\begin{equation}
E = cp^{0} \label{5-40}
\end{equation}
と定義すれば、\(E\)は次式であることが導けます。
\begin{equation}
E = m_{0}c^{2}\cfrac{1}{\sqrt{1-β^{2}}} \label{5-41}
\end{equation}
この式により、速度が\(0\)(\(β=0\))でも質量は\(m_{0}c^{2}\)のエネルギー\(E\)を持っています。
これを静止質量エネルギーといいます。
(3)運動方程式の共変形式
① 外力が作用しない自由粒子の運動
ニュートンの運動方程式(\(\cfrac{dp}{dt}=f=0\))において、時間\(t\)を固有時間τ、運動量を4元運動量に置き換えると次式が得られます。
\begin{equation}
\cfrac{dp^{i}}{dτ} = 0 \label{5-42}
\end{equation}
上式は、\(p^{i}\)が反変ベクトル、τがスカラーであるため、共変となります。
上式を積分して得られる\(p^{i}=一定\)、の式の空間成分(\(μ=1,2,3\))は
\begin{equation}
p^{μ} = \cfrac{m_{0}}{\sqrt{1-β^{2}}}v^{μ} = \mathrm{(一定)} \label{5-43}
\end{equation}
であり、運動量保存の式となります。
上式は、非相対論的極限(\(|β|\simeq 0\))では、ニュートン力学の運動量保存式(\(mv^{μ}=一定\))に一致します。
また、\eqref{5-40}より
\begin{equation}
cp^{0} = E = \mathrm{(一定)}\label{5-44}
\end{equation}
はエネルギー保存式を表しています。
非相対論的極限(\(|β|\simeq 0\))では、ニュートン力学のエネルギー保存式(\(\cfrac{\ 1\ }{2}mv^{2}=一定\))に一致します。
② 外力が作用する粒子の運動
外力が4元ベクトル\(f^{i}\)として与えられていれば、ニュートンの運動方程式の共変形式は次式となります。
\begin{equation}
\cfrac{dp^{i}}{dτ} = f^{i} \label{5-45}
\end{equation}
したがって、外力を4元ベクトルとして表すことができれば上式が適用できますが、
外力を4元ベクトルで表すことができなければ上式は適用できません。
現在知られている力では重力のみが4元ベクトルで表すことができないため、
重力が作用する空間は特殊相対性理論の適用範囲外となります。
そこで、それを解決すべく、一般相対性理論が誕生しました。
(4)4元力の例ー電磁気力
電磁場中で電荷\(Q\)を持つ荷電粒子の非相対性運動方程式は次式で表されます。 \begin{equation} \cfrac{d}{dt} \begin{pmatrix} p_{x} \\ p_{y} \\ p_{z} \end{pmatrix} = Q \begin{pmatrix} E_{x} \\ E_{y} \\ E_{z} \end{pmatrix} + Q \begin{pmatrix} \ 0\ & B_{z} & -B_{y} \\ -B_{z}\ & 0 & B_{x} \\ B_{y} & -B_{x} & 0 \end{pmatrix} \begin{pmatrix} v_{x} \\ v_{y} \\ v_{z} \end{pmatrix} \label{5-46} \end{equation} 上式で、時間\(t\)を固有時間τに置き換え、速度\(v^{μ}\)を4元速度\(u_{i}\)に拡張すると、次式が得られます。 \begin{equation} \cfrac{d}{dτ} \begin{pmatrix} p^{0} \\ p^{1} \\ p^{2} \\ p^{3} \end{pmatrix} = Q \begin{pmatrix} \ 0\ & \cfrac{1}{c}E_{x} & \cfrac{1}{c}E_{y} & \cfrac{1}{c}E_{z} \\ -\cfrac{1}{c}E_{x} & 0 & B_{z} & -B_{y} \\ -\cfrac{1}{c}E_{y} & -B_{z} & 0 & B_{x} \\ -\cfrac{1}{c}E_{z} & B_{y} & -B_{x} & 0 \end{pmatrix} \begin{pmatrix} u_{0} \\ u_{1} \\ u_{2} \\ u_{3} \end{pmatrix} \label{5-47} \end{equation} ここで、\(u_{i}\)は4次元速度を次式のように共変ベクトルとして表したものです。 \begin{equation} u_{i} = η_{ij}u^{j} = \begin{pmatrix} -\cfrac{dx^{0}}{dτ} \\ \ \cfrac{dx^{1}}{dτ} \\ \ \cfrac{dx^{2}}{dτ} \\ \ \cfrac{dx^{3}}{dτ} \end{pmatrix} \label{5-48} \end{equation} また、\eqref{5-47}右辺の行列は、\eqref{5-30}における電磁場のテンソル(反変テンソル)\(f^{ij}\)であるため、 運動方程式は次式で表されます。 \begin{equation} \cfrac{dp^{i}}{dτ} = {f^{i}}_{EM} \label{5-49} \end{equation} ここで、\({f^{i}}_{EM}\)は次式で表される電磁力の4元力です。 \begin{equation} {f^{i}}_{EM} = Qf^{ij} \cdot u_{j} \label{5-50} \end{equation}
【文献】
(1) 佐藤勝彦:”岩波基礎物理シリーズ 相対性理論”, p.x, 新装版、2023年5月15日、岩波書店
(2) 見城尚志、佐野茂:”幾何で見える必ずわかる一般相対性理論”、pp.216-217、初版、2022年10月7日、株式会社技術評論社。