1 ニュートン力学で未解決であった現象
1.1 水星の近日点移動
惑星の軌道は、ニュートン力学によれば、2次元平面上の楕円、円、双曲線又は放物線(円錐曲線)となります。
この惑星軌道を極座標(\(r, \varphi\))で表した微分方程式は
\begin{equation}
\cfrac{d^{2}u}{d\varphi^{2}} + u = \cfrac{GM}{q^{2}} \label{a1}
\end{equation}
であり、その一般解は下記のとおりです。
\begin{equation}
u = A\cos\varphi + B\sin\varphi + \cfrac{GM}{q^{2}} \label{a2}
\end{equation}
ここで、
\(u = 1/r\)
\(G\)(万有引力定数)= 6.67 x 10-11 (N•m2/kg2)
\(M\)(太陽の質量) = 1.98892x1030(kg)
\(q\)(角運動量)
\(A, B\):定数
また、太陽の中心からの惑星の近日点(惑星軌道上で太陽に最も近づく点)までの距離\(r_{0}\)は次式で表されます。
\begin{equation}
r_{0} = \cfrac{\rho}{1 + \sigma\ } = \cfrac{q^{2}}{GM(1 + \sigma\ )} \label{a3}
\end{equation}
ここで、\(\rho\)(\( = q^{2}/GM\))は円錐曲線の半通径又は半直弦と呼ばれるパラメータです。
\(\sigma\)は離心率と呼ばれ、軌道の形により以下の通りです。
円 :\(\sigma = 0 \)
楕円 :\( 0 \lt \sigma \lt 1 \)
放物線:\(\sigma = 1 \)
双曲線:\(\sigma \gt 1 \)
楕円軌道を描く太陽系の惑星は、2つの焦点のどちらかを太陽とすることが観測され、ニュートン力学による計算値とほぼ一致していたが、
太陽に最も近い水星については、わずかにずれていました。
具体的には、水星の楕円軌道が図1(理解の容易のため実際の水星の近日点移動よりも大きく描かれています。)にように毎年少しずつずれていき、
そのずれを近日点の移動量で評価すると、100年間に574秒(1秒=1/3,600度)すなわち0.159度であることがわかっていました。
さらに、このズレ量の大部分は、他の惑星の重力の影響であることも解明されていましたが、
43秒(0.0119度)のずれ量については、解明できていませんでした。
ちなみに、0.0119度(=0.0119度 x πラジアン/180度)= 0.000208ラジアンですから、この角度に対応する1km先の距離は、
約0.208m(=1,000m x 0.000208ラジアン)すなわち21cmと非常に微小です。
現在から100年以上前の観測技術、解析技術には感嘆します。
このずれは非常にわずかですが、当時は、その理由が説明できないため、太陽系にはまだ未発見の惑星があり、
その惑星による重力の影響を受けているのではないかとその未発見の惑星の発見に注力していましたが、発見できない状態でした。
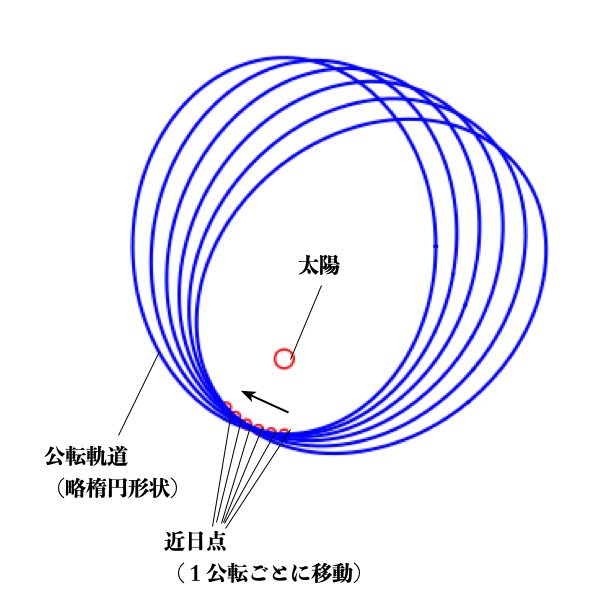
図1 近日点移動
1.2 強い重力場中での光の湾曲
ニュートンの万有引力の法則は、質量を持つ物体の間で作用するため、質量を持たない光は本来、重力を受けないはずです。
しかし、日食の観測により、太陽の背後の星からの光が観測されました(図2参照)。

図2 太陽の背後にある星からの光跡の太陽の重力による曲がり