2 曲がった空間
相対性理論成立前においては、質量\(M\)の物体からの万有引力(重力)を受けて質量\(M\)から距離\(r\)にある物体(質料\(m\))の運動は、
以下の万有引力の法則による重力\(F\)により計算できると考えられていました。
\begin{equation}
F = G\cfrac{mM}{r ^2} \label{b1}
\end{equation}
ここで、\(G\)(万有引力定数)\(=6.67\times 10^{-11}\) N•m2/kg2
しかし、アインシュタインは、特殊相対性理論で導入した時空(時間と空間はそれぞれ独立したものではなく、
相互に関連するもの)をさらに発展させて、空間が(強い)重力の影響を受けて歪み、
曲がった空間を形成するものであると考えました。
その結果、重力を受ける空間(重力場)を運動する物体は、曲がった空間内を運動するために、
その曲がった空間に対して最短経路(測地線)を移動(”進行”)することになるはずと考えました。
また、光は質量を持たないため、従来のニュートンの万有引力の法則では重力が作用しないはずですが、
光も、物体と同様に曲がった空間に沿って進行するために曲がることとなると考えました。
曲がった空間座標は、現実には3次元となりますが、理解の容易のため、
本章では2次元の空間座標としての曲がった空間(本章では曲面と呼ぶこととします)を中心として説明します。
曲面の説明に入る前に、先ず、2次元の平坦な空間(本章では、平面と呼ぶこととします)の代表的な三角形の性質として
三角形の内角の和が180度(\(\pi\)ラジアン)及び三平方の定理を図1に示しておきます。
平面としてのこれらの性質は、読者の皆様が中学や高校(の数学や幾何)で学習したものであり、日常生活や通常の業務に使用されているものとなります。

図1 三角形の代表的な性質(平面)
2.1 球面
(1)概要
現在では、人工衛星等による宇宙から撮影した画像から地球が球体であることを実感できますが、
大昔の人々は(天体現象等から地球は丸いと考えた学者も存在したものの)地球(地面)は平らと考えていました。
それは、地球が我々の日常生活の範囲に比べて非常に大きいので、現実には地面は平らと認識されるためであり、
また、宇宙空間という地球外から観察できるようになったためです。
このことは、宇宙空間についても同様であり、地球において宇宙空間が平坦か曲がっているかを直接的に判断するのは非常に困難であり、
物理現象等が平らな空間か曲がった空間かのどちらに整合しているかにより判断されることになります。
そこで、2次元の曲がった空間の代表である球面について、その性質等について説明します。
イメージとしては、地球儀を考えていただければ理解しやすいので、地球儀と同様な表現で表した球面を図2に示します。
球面において任意に中心軸を設定し、中心軸と球面との2つの交点(極点)をP、Qとし、
この2つの極点P、Qを結び球面上の線を経線と呼ぶこととします。
このとき、経線は大円(球面の中心点を中心とする円であり、その半径は球面の半径と等しい)となります。
一方、中心軸に垂直な平面で球面を輪切りにしたときに、輪切りにより球面に描かれた円を緯線と呼ぶこととし、
球の中心点Oを緯線を特に赤道と呼ぶこととします。
したがって、緯線は赤道のみが大円であり、赤道以外のものは小円(球面の中心点を通らない円であり、
その半径は球面の半径より小さい)となります。
なお、地球の場合は、中心軸は地軸と特定されますが、一般的な球面の場合は、中心軸は任意ですので、
以下の幾何学的な説明内容は一般的に成立します。
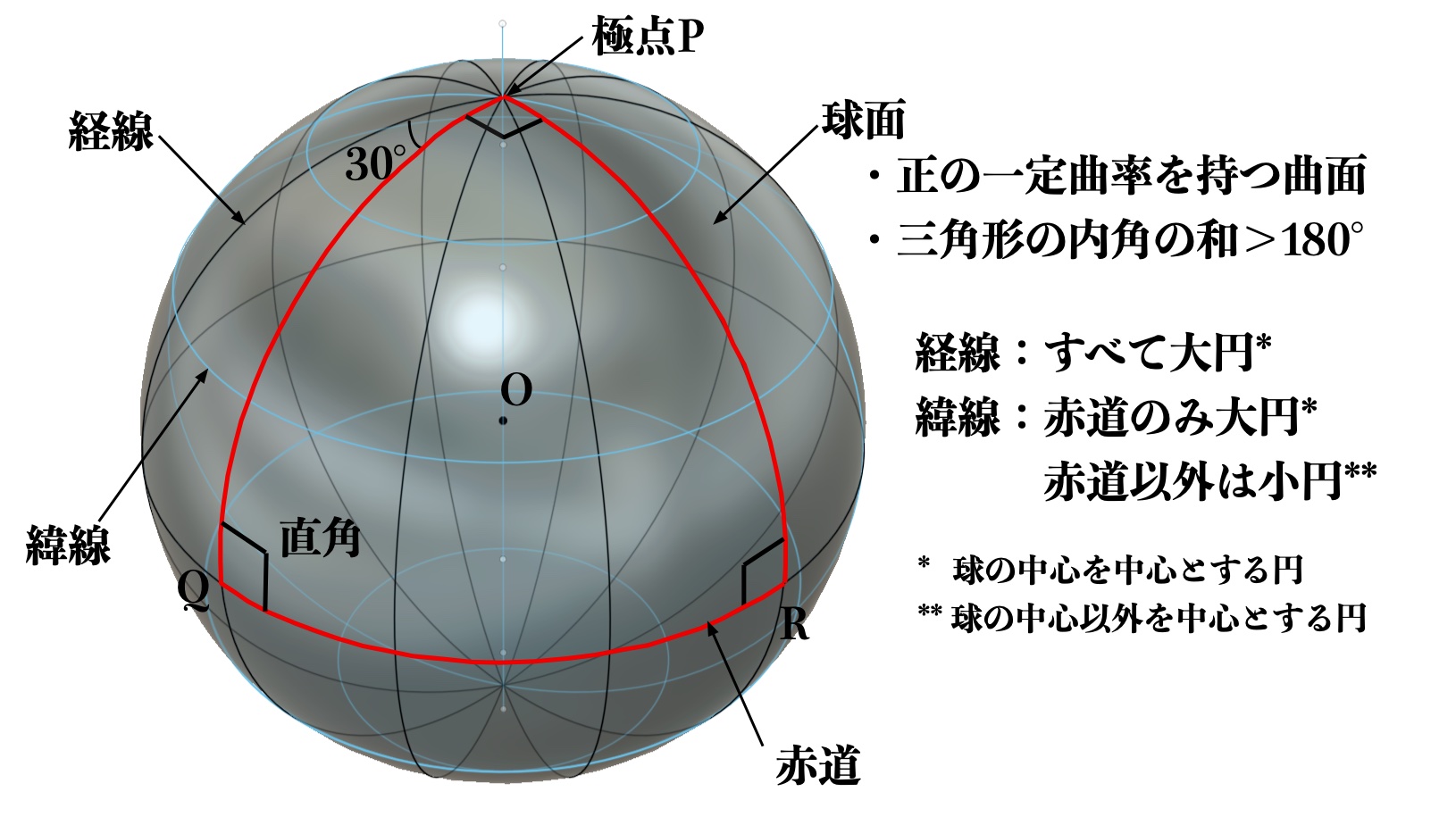
図2 球面
(2)測地線
曲がった空間における重要な概念の一つが測地線です。
測地線とはその空間における2点間の最短線をいい、平坦な空間(平面)における直線(線分)に相当しますが、
曲がった空間(曲面)ではその2点を通る曲面上に沿った最短線となるため、三次元的には曲線となります。
したがって、球面の場合には、2点間の最短線はその2点を通る大円(球の中心(球心)を通る平面による球面の切断線)となるため、
例えば、図3における緯線上の2点A、B間の測地線は、その緯線上ではなく、2点A、Bを通る大円上のものとなります(図3参照)。
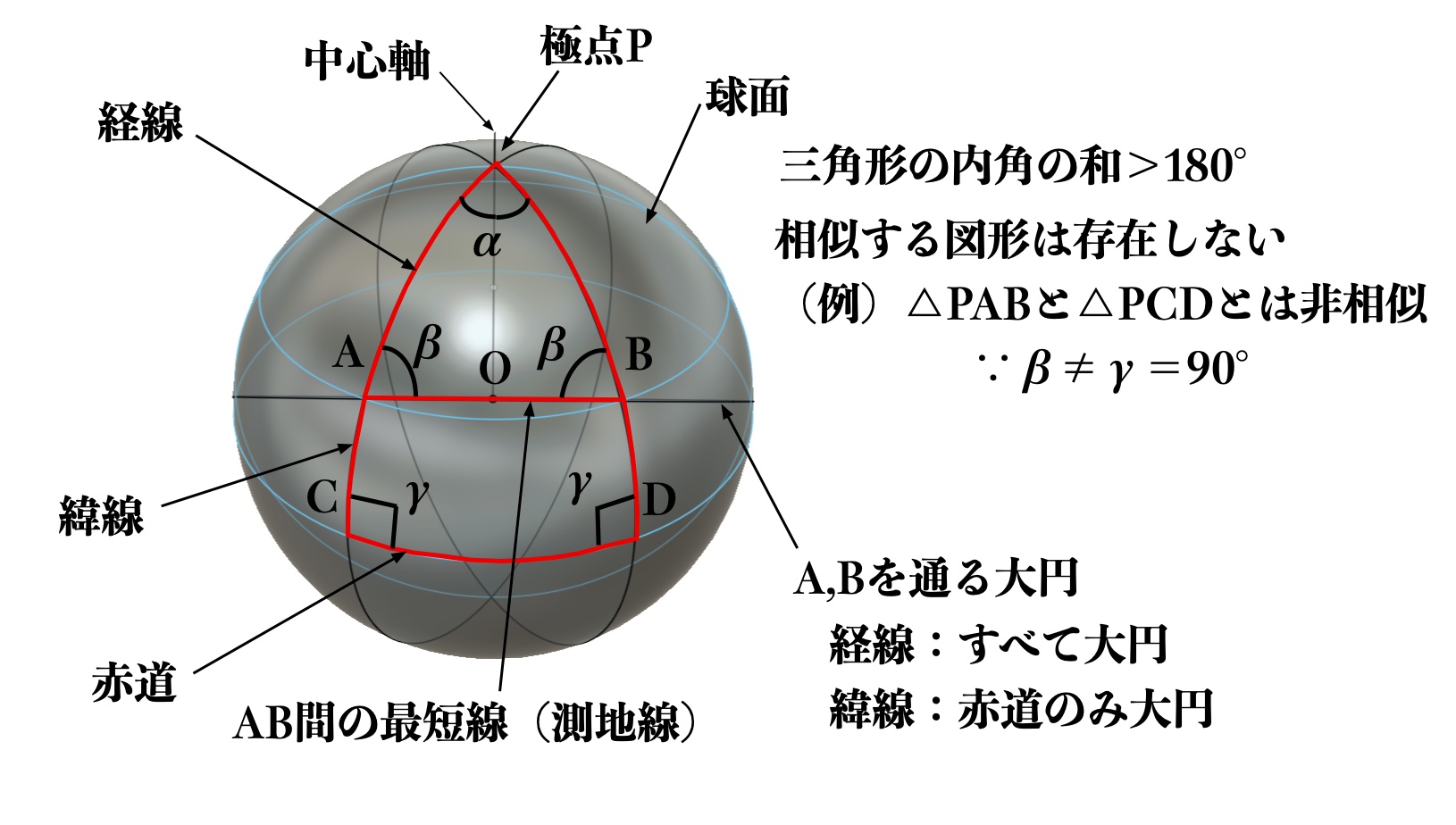
図3 球面上の三角形、測地線等
(3)三角形の内角の和
球面上の三角形は、3つの辺は測地線である大円で連結されるため、その内角の和は2直角より大きくなります。
例えば、極点Pにおいて直角に交わる2つの経線を赤道まで延長して赤道との交点をQ、Rとしたときに
3点P、Q、Rで形成される三角形PQRのそれぞれの内角はいずれも直角となるので、
三角形PQR(大円の円周の4分の1の長さの測地線で形成される三角形)の内角の和は3x90°=270°(3直角)となります(図2参照)。
このように、球面上の図形(幾何)は平面上の図形(幾何)と異なり、例えば、球面上で、ある地点(出発点)Aからある方向に距離dの地点Bに進み、
地点Bで測地線BA方向に振り返って右側60°の方向へ距離dの地点Cまで進み、地点Cで測地線CB方向に振り返って右側60°の方向へ距離dの地点Dへ進んだ場合には、
地点Dは出発点Aとは一致しない点(終点)Dに到着することになります(図4参照)。
球面上の正三角形の各内角は60°より大きい(例えば65°)ため、地点B、Cで60°の方向へ向かうと、
到達地点Dは、出発地点Aに対して進行方向の左側にずれることとなります。
2次元空間である球面上の観察者からは、球面上の図形等を観測することによりその空間が曲がっているという事実を認識できることになります。
したがって、球面の曲率は、上記のように測定した終点Dの出発点Aからの偏位により評価できることとなります。
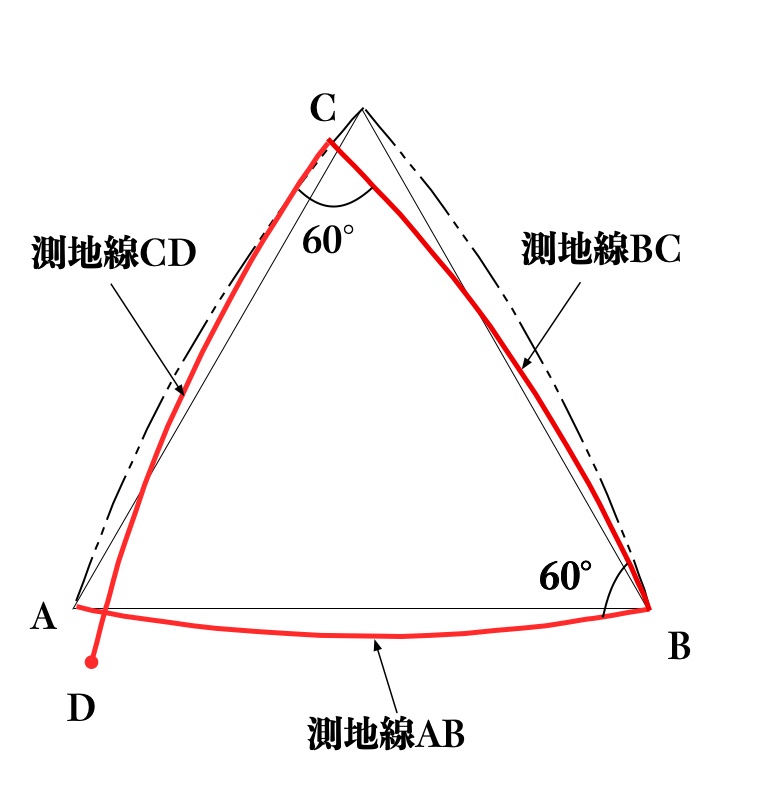
図4 球面上の正三角形、その正三角形の経路に沿って移動したときの経路
(4)相似な図形
三角形の大きさにより三角形の各内角の大きさが異なるため、球面については、相似形が存在しません(図3参照)。
球面上の直角三角形については、平面上の直角三角形の三平方の定理に相当するものとして図5に示すような関係式が存在します。
この関係式において球面が平面に近づくと、近似的に三平方の定理になります。
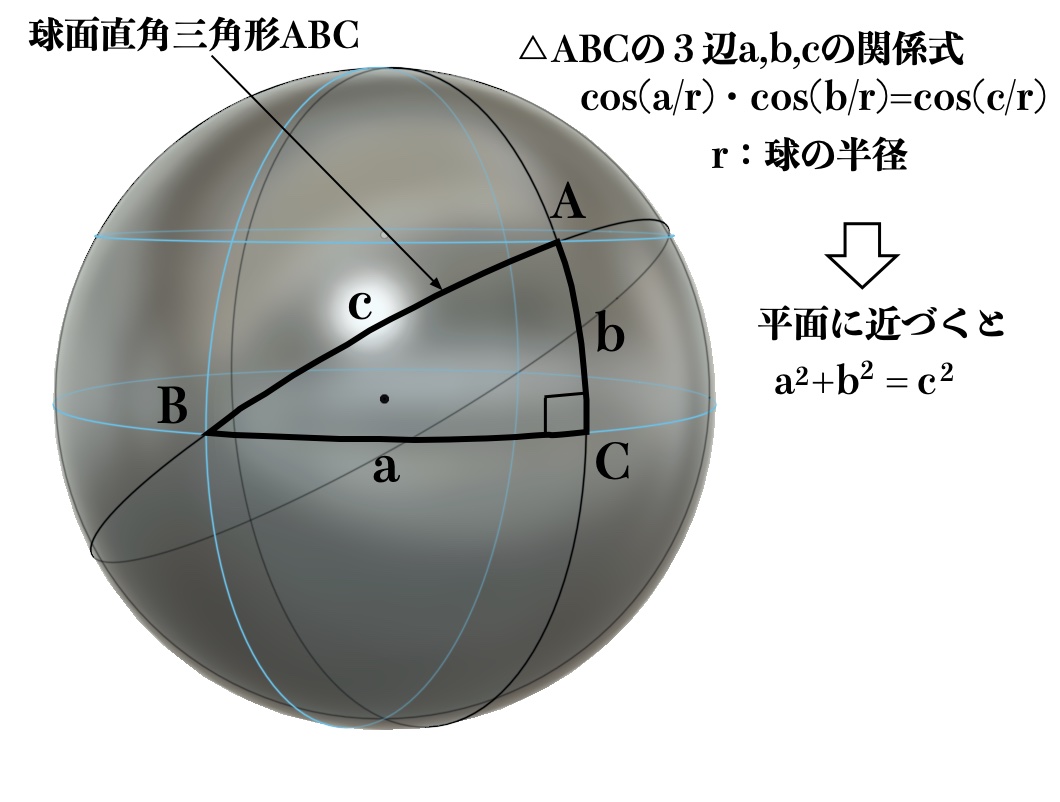
図5 球面直角三角形の3辺の関係式
【コラム1】球面三角形の性質
球面三角形(A、B、Cを連結する3本の測地線により形成された△ABC)の内角の和が2直角(\(\pi\)ラジアン)
より大きいことを下記図を使用して示します。
ラジアンとは、半径1の円の円弧の長さでその円弧に対応する中心角で角度を表示する方法(弧度法)による単位であり、
円周(360°)は \(2\pi\)ラジアンとなります。
球心Oに対してA、B、Cのそれぞれに対称の位置にある点をA'、B'、C'とします。
なお、以下の検討では、球面上の部分の表面積を鉤括弧「[ ]」で表すものとします。
例えば、[△ABC]は、△ABCの表面積を表します。
△A'B'C'は球心Oに対して△ABCと対称なので、△A'B'C'と△ABCとは合同であるため、
∠A'=∠A=\(\alpha\)、∠B'=∠B=\(\beta\)、∠C'=∠C=\(\gamma\)、[△A'B'C']=[△ABC]となります。
測地線BAB'、BCB'は端点B、B'を共通として、直線BB'は球の中心点Oを通るので、
測地線ABA'と測地線ACA'とに囲まれた球面二角形ABA'CA(図a1で赤線表示)の表面積[ABA'CA]は、
\begin{align}
\mathrm{[ABA'CA]} &= 球の表面積(4πr^{2})\x \frac{\alpha}{\ 2\pi\ } \notag \\
&= 2\pi r^{2} \notag
\end{align}
となる一方、[△ABC]+[△A'BC]であるため(図a1参照)
\[
\mathrm{[△ABC]} + \mathrm{[△A'BC]} = 2\alpha r^{2} \tag{a1}
\]
となります。
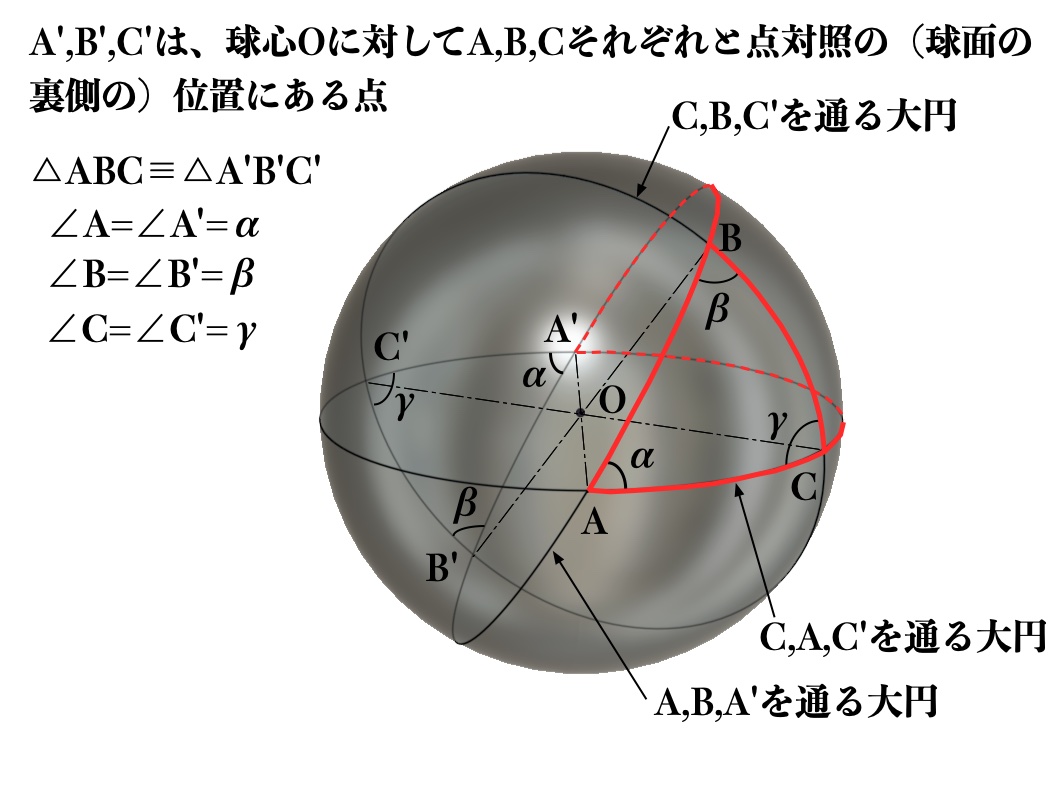
図a1 球面二角形ABA'CAと球面三角形ABC
同様にして、測地線CBC'とCAC'とに囲まれた球面二角形CBC'AC(図a2で青線表示)の表面積[CBC'AC]、及び測地線BA'B'とBC'B'とに囲まれた球面二角形BA'B'C'B(図a3の黄線表示)の表面積[BA'B'C'C]は、それぞれ、2γr2、2βr2となるため、
\[
\mathrm{[△ABC]} + \mathrm{[△ABC']} = 2\gamma r^{2} \tag{a2}
\]
\[
\mathrm{[△A'BC']} + \mathrm{[△A'B'C']} = 2\beta r^{2} \tag{a3}
\]
となります。
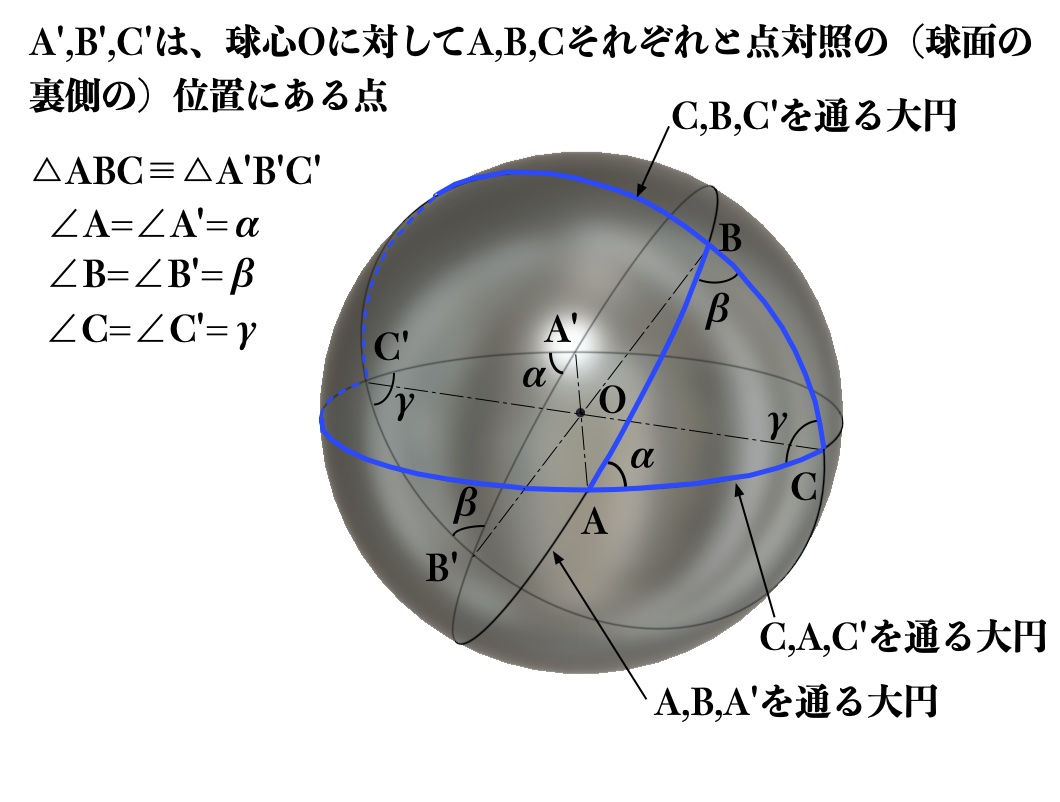
図a2 球面二角形CBC'AC

図a3 球面二角形BA'B'C'B
図a1から大円AC'A'CAより上の半球の表面積Sは、\(4\pi r^{2}/2=2\pi r^{2}\) である一方、図a1〜a3より、
△ABCと△A'B'C'とが合同であること及び(a-1)〜(a-3)を利用すると、Sは以下のとおりとなります。
\begin{align}
S &= \ \mathrm{[ABA'CA]} + (\mathrm{[CBC'AC]}-\mathrm{[△ABC]}) + \mathrm{[BA'B'C'B]}\ - \mathrm{[△A'B'C']} \notag \\
&= \ \mathrm{[ABA'CA]} + \mathrm{[CBC'AC]} + \mathrm{[BA'B'C'B]}\ - 2\ \mathrm{[△A'B'C']} \notag \\
&= 2\pi r^{2}\ + 2\beta r^{2}\ + 2\gamma r^{2} - 2 \mathrm{[△ABC]} \notag
\end{align}
となるため、
\[
2\pi r^{2} = 2\ (\alpha +\beta + \gamma )r^{2} - 2 \mathrm{[△ABC]}
\]
となり、これより以下の式が得られます。
\[
(\alpha + \beta + \gamma ) - \pi = \frac{\ \mathrm{[△ABC]}\ }{r^{2}} \tag{a4}
\]
又は、
\[
\frac{\ (\alpha + \beta + \gamma ) -\pi }{\mathrm{[△ABC]}} = \frac{1}{\ r\ ^{2}\ } \tag{a5}
\]
が得られます。なお、これらの式をガウス・ボンネの定理といいます。
(a4)式の右辺は正となるため、
\[
\alpha + \beta + \gamma \gt \pi \mathrm{(2直角)} \tag{a6}
\]
となります。これにより、球面三角形ABCの内角の和は2直角より大きくなることが示されました。
(a6)より、内角の和(α+β+γ)は、球の半径\(r\)が小さくなるほど2直角より大きな値になり、
逆に\(r\)が大きくなると2直角に近づきます(\(r\)が無限大になると平面になるので、内角の和が2直角になります)。
\(1/r^{2}\)は球面の曲がり度の指標となる曲率\(K\)となります。ただし、球面の半径\(r\)は、3次元世界にいる観察者からは観測可能ですが、
2次元世界である球面上にいる観察者にとっては、\(r\)を直接観測することができません。
ところが、(a5)の左辺の以下の量は、三角形ABCの各内角\(\alpha、\beta、\gamma\)及び面積[△ABC]を測定することにより、求めることができます。
\[
\frac{\ (\alpha + \beta + \gamma ) - \pi }{\mathrm{[△ABC]}}
\]
したがって、上記の量は球面上の世界における観察者にとっての曲率\(K\)(\(=1/r^{2}\))として定義することができます。
なお、球面三角形△ABCの面積[△ABC]は次式で与えられるため、球面上の観測値により算出することができます。
\[
2 \sin\frac{\mathrm{[△ABC]}}{2}=\frac{\sqrt{\sin s\ \sin(s-a)\ \sin(s-b)\ \sin(s-c)}}{\cos\cfrac{a}{2}\ \cos\cfrac{b}{2}\ \cos\cfrac{c}{2}} \tag{a7}
\]
ただし、\(2s = a + b + c\)(\(a, b, c\)は△ABCの3辺の長さ)
(a6)式をカニョールの公式といい、△ABCが小さいときは、次式で表される平面三角形の面積\(S\)の公式(ヘロンの公式)で近似できます。
\[
S = \sqrt{s(s-a\ )(s-b\ )(s-c\ )} \tag{a8}
\]
2.2 擬球面
正の一定曲率を持つ球面と対照的に負の一定曲率を持つ曲面が擬球の表面(擬球面)です。
擬球面は、図6に示されるように中心軸に対して回転対称な曲面を有しており、中心軸を含む平面で切断した曲線(経線)は双曲線で形成されています。
中心軸に垂直な平面で切断した曲線(緯線)は円であり、経線とは直角に交わっています。
擬球面上の三角形の内角の和は2直角より小さくなります(コラム2参照)。
擬球面を局部的に観察すれば、図7に示されるように鞍型の表面(鞍型面)となっています。
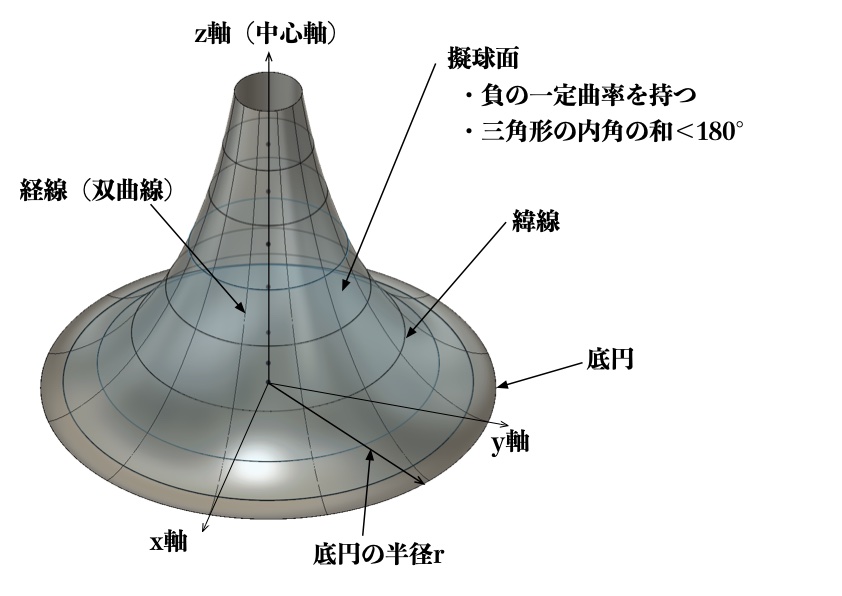
図6 擬球面
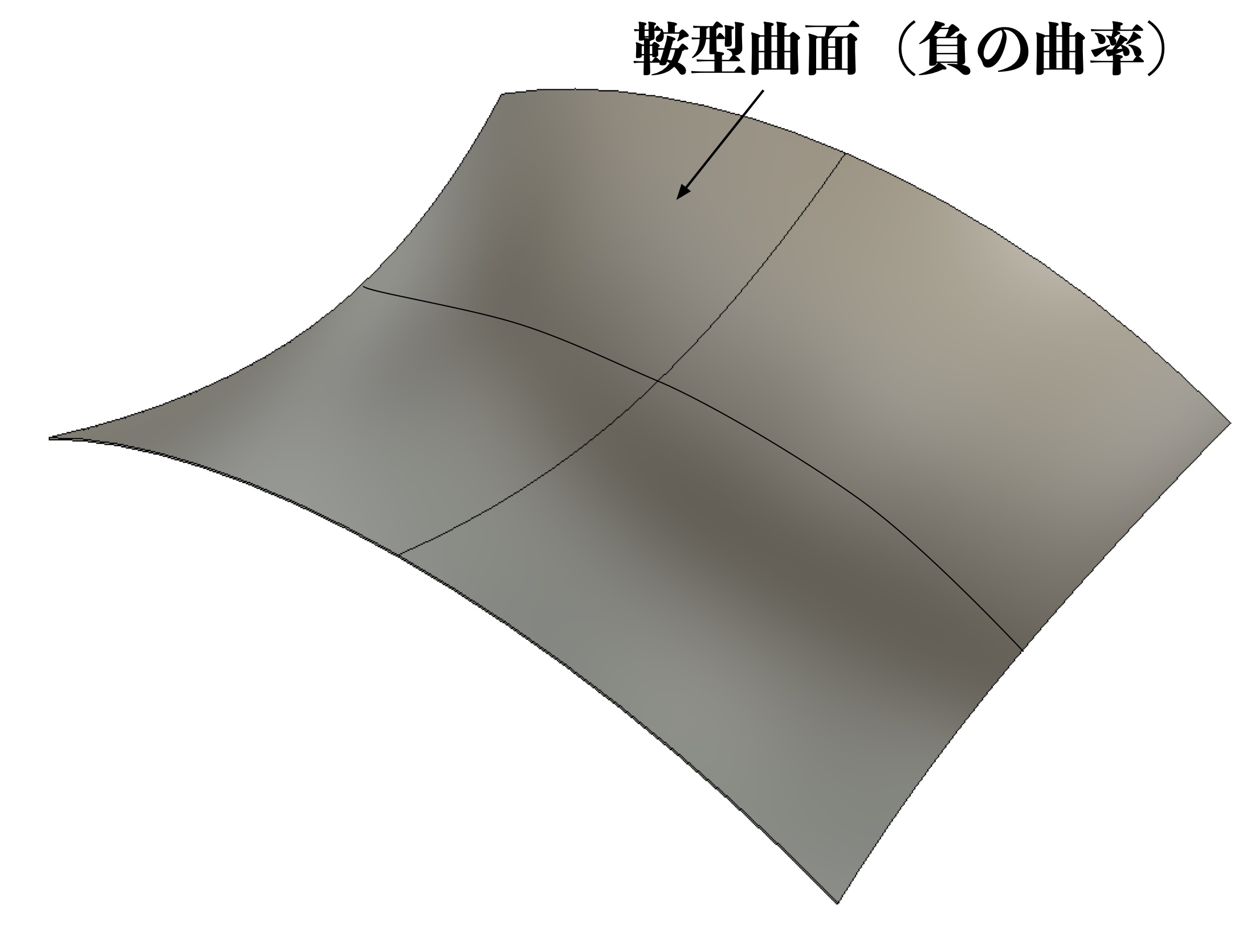
図7 鞍型面
【コラム2】擬球面の性質等
擬球面の形状は、\(x-z\)軸断面において次式の双曲線の \(z\geqq 0\) の範囲を\(z\)軸周りに360°回転することにより生成される面となります(図6参照)。
\[
z = r\ \bigl (\ log\frac{1+\sqrt{1-X^{2}}}{X}-\sqrt{1-X^{2}}\quad\bigr) \tag{b1}
\]
ただし、\(X = x/r\)
したがって、底円(\(z=0\)における円)の半径\(r\)が異なる擬球どうしは相似形となります。
例えば、底円の半径が \(r_{1}\)と\(r_{2}\) である2つの擬球の相似比率は \(r_{1}\):\(r_{2}\) となります。
底円の半径\(r\)の擬球面における(測地線で形成された)三角形△ABCについても次式で表現される面積の定理(ガウス・ボンネの定理)が成立します。
\[
π\ - (\alpha + \beta + \gamma ) = \frac{\ \mathrm{[△ABC]}\ }{r^{2}} \tag{b2}
\]
又は、
\[
\frac{π\ - \ (\alpha + \beta + \gamma )\ }{\mathrm{[△ABC]}} = \frac{1}{\ r\ ^{2}\ } \tag{b3}
\]
(b2)式右辺が正であるため、(b2)式より、
\[
\alpha + \beta + \gamma \lt \pi \mathrm{(2直角)} \tag{b4}
\]
となり、擬球面三角形の内角の和は2直角より小さくなります。
∠Cを直角とする擬球面直角三角形ABC(A、B、Cの対辺をそれぞれ\(a\)、\(b\)、\(c\))についての三平方の定理は次式で表されます。
\[
\cosh\frac{a}{r}\ \cosh\frac{b}{r} = \cosh\frac{c}{r} \tag{b5}
\]
ここで、\( \cosh(\ ) \) は、双曲線関数であり、次式で表されます。
\[
\cosh(x) = \frac{e^{x} + e^{-x}}{2}
\]
2.3 その他の曲面
前記の球面又は擬球面は、それぞれ正又は負の一定曲率を持つ曲面でしたが、一般的には曲面は位置により正負を含めて曲率が異なります。
楕円体の表面(楕円面)はすべての位置で正の曲率ですが、位置により曲率の値は異なります。楕円面の特別なものが球面と考えることができます。
図8に示すトーラスの表面(トーラス面)は、内周側の面(内周面)において負曲率、外周側の面(外周面)において正曲率であり、
トーラスの上面、下面の内外周の境界にあたる円周上の曲率は0となっています。
これに対して、円筒面は三次元空間の観察者からは曲がった2次元空間となりますが、その曲率は0となります。
これは、円筒面は、上記に紹介した空間と異なり、円筒の中止軸に平行な直線の一つで切り開いて展開することにより平面とすることができ、
その結果、円筒面上の図形等が平面上の図形等と完全に一致するからです。
したがって、2次元空間である円筒面上の観察者は、円筒面の円周方向に沿って移動して元の位置に戻るという行動を取らずに、
観察者の周辺の観察をする限り、円筒面であること(すなわち曲がった空間あること)が確認できず、平面上に存在しているとの認識となります。
そこで、円筒面のように3次元空間からの観測者からは曲がった空間ですが、
2次元空間である円筒面の観察者による局所観測だけでは平面と認識せざるを得ないものは曲がった空間の対象から除外することとしています。
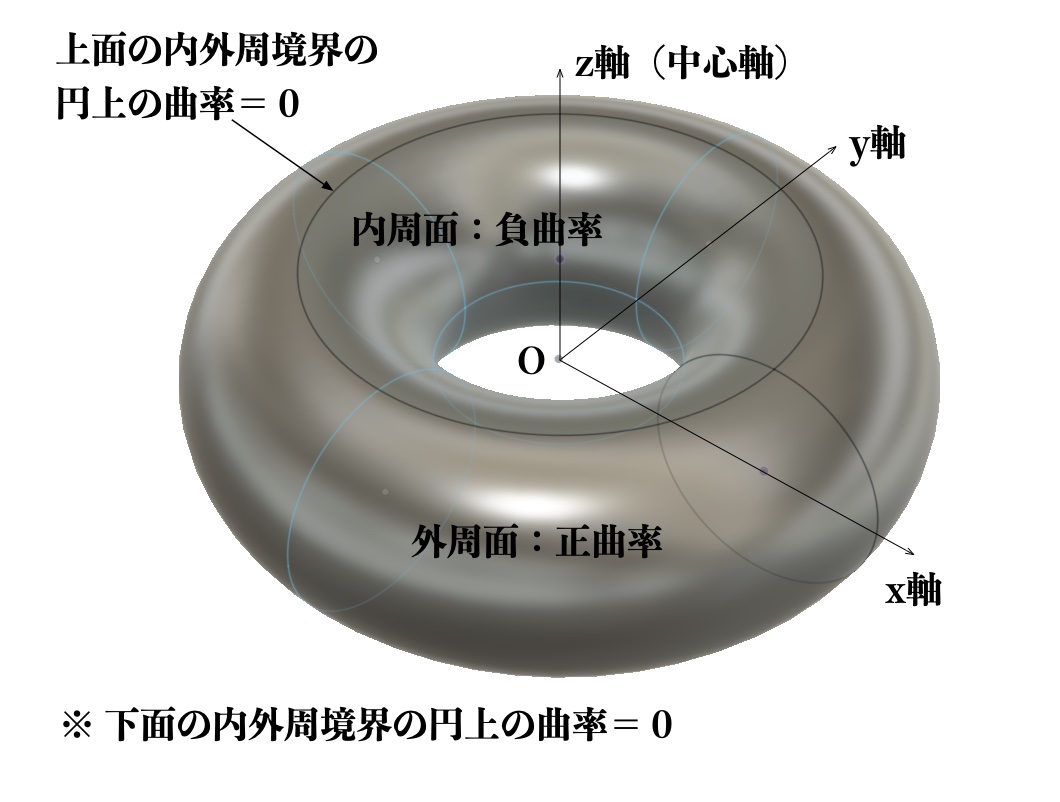
図8 トーラス面
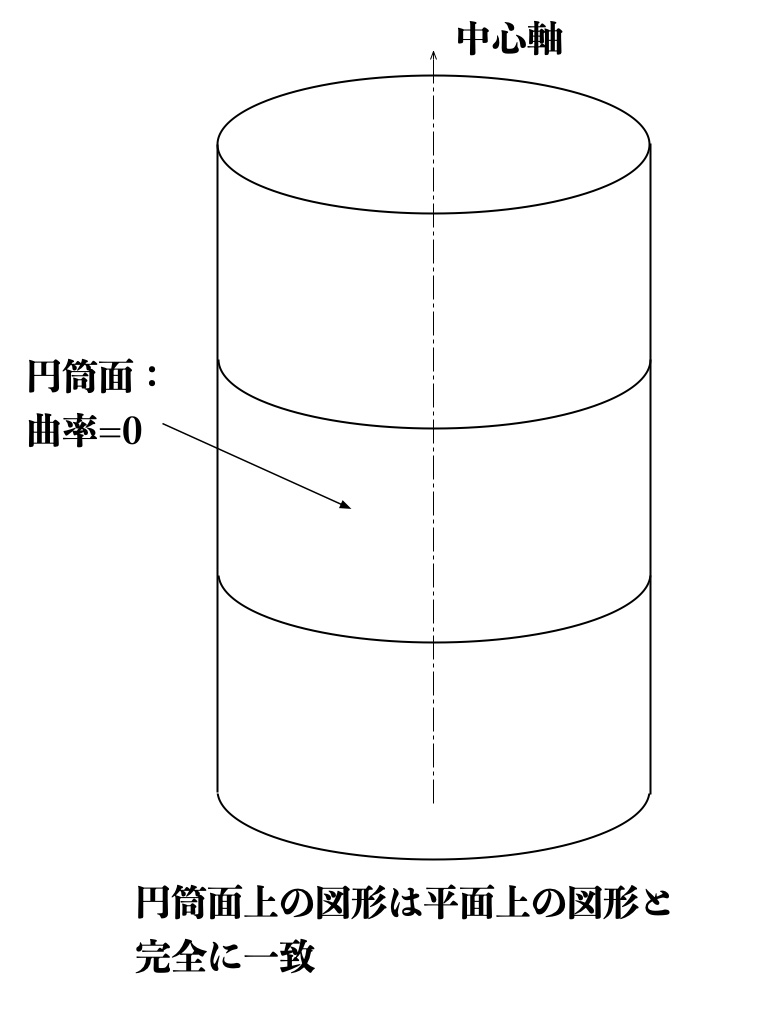
図9 円筒面