3 等価原理
3.1 等価原理の導入
図1のように地上で自由落下するエレベータを想定します。
高層階からエレベータを自由落下させると、エレベータ内で観察すると、内部の物体は空中に浮遊して重力の作用を受けていない(エレベータ内は無重力状態)と観察されます。
このような自由落下するエレベータに窓等がなく外部との関係が把握できなければ、室内の観察者は、宇宙空間で静止(又は一定速度で飛行)して無重力な宇宙船内(慣性系)にいると同じ状態となります。
これは、まさにエレベータを自由落下させることにより、重力の作用する地球上に、局所的に重力の作用しない慣性系を形成させることができます。
このように、重力の作用する空間において、物体に重力により加速度(重力加速度)で運動する空間を形成させて、その空間の内部の重力を消し去って局所慣性系にすることを等価原理といいます。
地上から約400km上空の地球のまわりを回っている国際宇宙ステーション(ISS)は地球の重力を受けているが、内部の空間は無重力です。これは、ISSが地球に向けて自由落下しているためです。
ニュートンが、リンゴは木から落ちるのに何故月は落ちないのかとの疑問から万有引力の法則を発見したことで有名な逸話のとおりです(月が慣性の法則によりそのまま一直線に進んで地球から離れて宇宙の彼方に飛び去ってしまわないのは(水平に投げたボールが落ちるのと同様に)月も地球の重力により落ちているためです)。
このことより、ISSは地球に対して自由落下していますが、ISS内作業している宇宙飛行士は内部空間が重力を受けていない慣性系であることが実感できます。
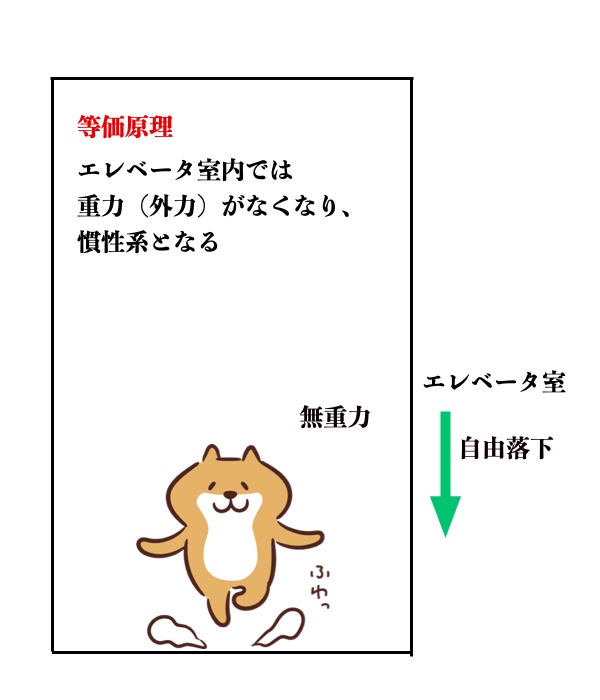
図1 等価原理(自由落下するエレベータ)
次に、地球の重力圏から脱出し、地球を含む天体からの重力の影響をほとんど受けない宇宙空間で移動する宇宙船を想定します。
この宇宙船が一定速度で巡航しているときは、宇宙船内は無重力であり慣性系となります(図2参照)。
一方、宇宙船が重力加速度\(g\)(=9.8m/s2)で加速しているときは、加速方向と反対方向に地上にいるときと同じ重力を受けることになり、
加速方向と反対方向の面が床となり、宇宙船の人は床に立ったり寝たり、船内の空中の物体は床には床に”落ちる”ことになります(図3参照)。
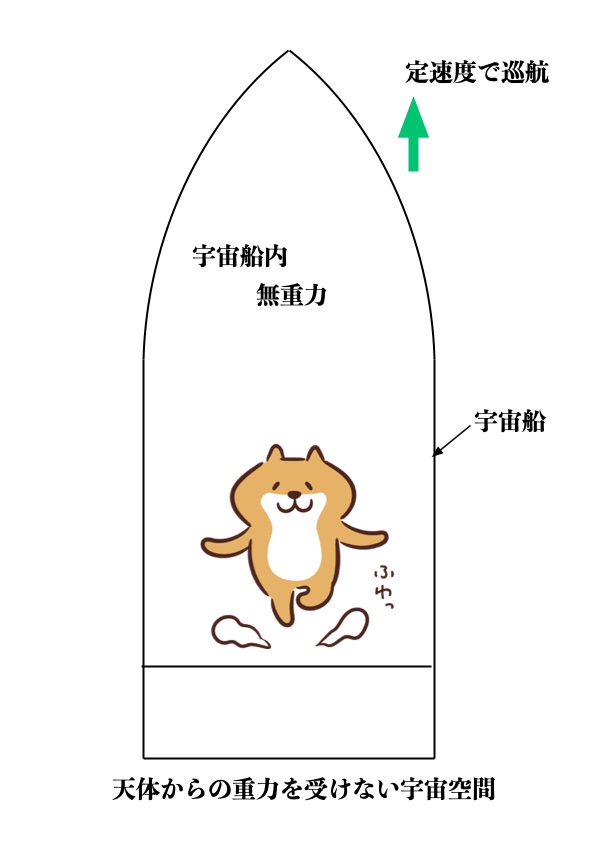
図2 定速度で巡航する宇宙船
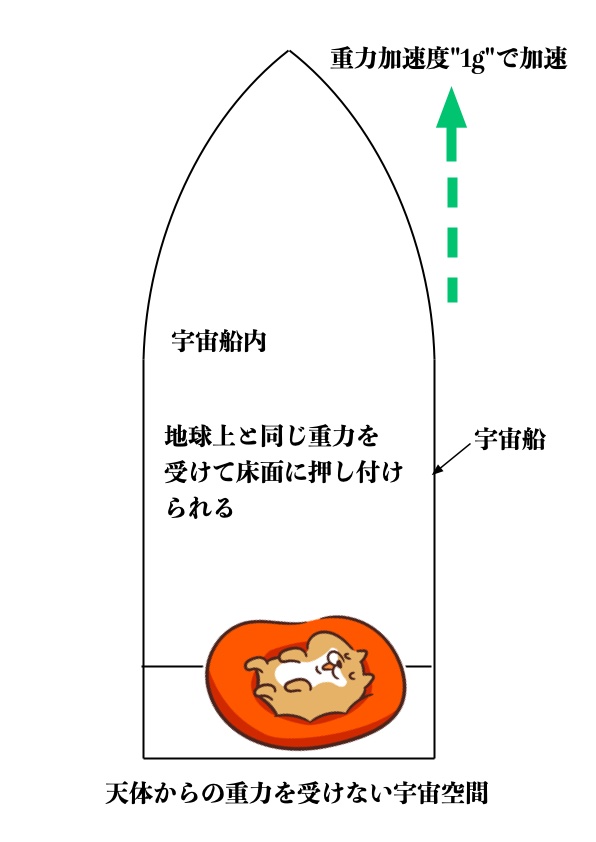
図3 重力加速度gで加速する宇宙船
【コラム3】アインシュタインの思考実験
アインシュタインは、この等価原理を利用して、自由落下するエレベータ内を水平に直進する光線の軌跡について、
次のような思考実験を行いました。
図c1の自由落下するエレベータの対向する壁面の同一水平位置に設定された一対の窓の一方(左側)から
ビーム光をエレベータ室に水平に入光して他方(右側)の窓から抜けるようにすると、ビーム光は室内では水平に直進すると観察されます。
一方、エレベータの外部から観察すると、光線はエレベータ、エレベータ室内の物体と同様に落下して(曲がって)
右方の窓から室外へ出るはずと考えられます。
そして、(最も単純に考えれば)水平に放出した物体と同様に、光線は放物線を描くであろうと考えました。
なお、このエレベータの思考実験により試算された重力による光線の変位は後の正しい計算による変位の1/3程度でした(【文献】(1))。
その原因の1つが重力の潮汐力(後記【コラム4】潮汐力参照)についての検討がされていなかったことと言われています
(文献(2))。
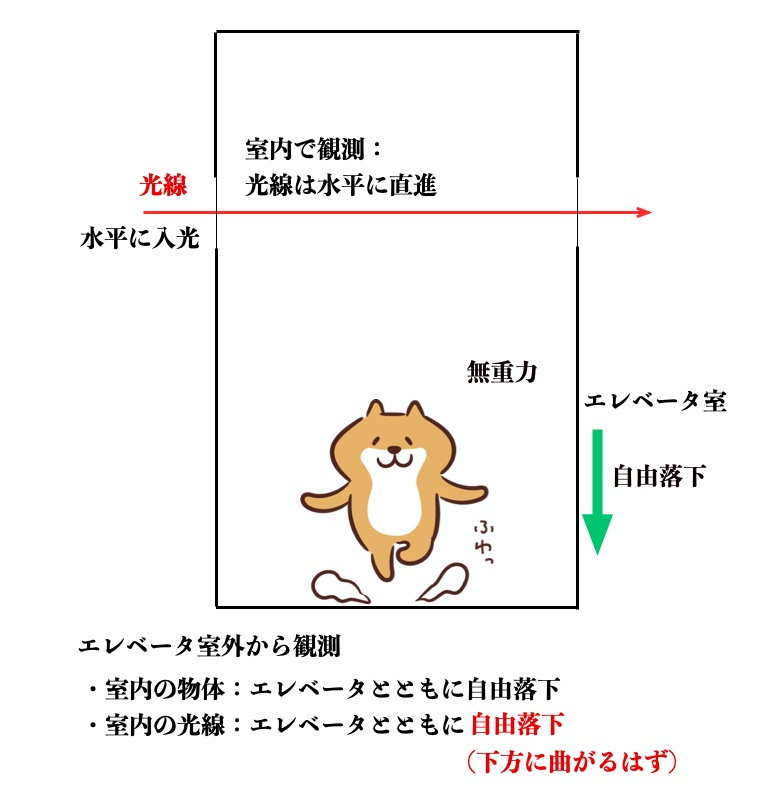
図c1 重力により光が曲がることの思考実験
【コラム4】潮汐力
等価原理により、自由落下する局所空間においては、その局所空間内の重力を無くした局所慣性系を形成することができます。
しかし、同じ高さにある2点A、Bの粒子が自由落下すると、A、B地球に中心に向けて落下するため、
落下に伴い2点A、B間の距離は接近していきます(図d1(a))。
また、自由落下中の複数の物体に作用する重力の大きさは一定ではなく、重力源に近いほど大きく、遠いほど小さくなります(万有引力の法則、(4)式参照)。
このため、図d1(b)の上側に描いた局所空間内にほぼ正方形ADBCの頂点に配置された粒子は、下端Dに最も大きな重力が作用し、
中間部のA、Bにそれより弱い重力、上端Cに最も弱い重力が作用するため、Dが最も早い速度で落下、A,Bがそれより遅い速度で落下、
Cが最も遅い速度で落下します。
また、A,B間の距離は自由落下に伴い、(a)のように接近します。
その結果、自由落下により四角形ADBCは縦長菱形形状の四角形A'D'B'C'に変形していきます(図d1(b))。
このように、重力の局所的影響を無くした局所慣性系において重力の非局所的影響を生じさせる現象を潮汐力といいます。
代表的な潮汐力現象は満干潮であり、月に向かって自由落下<注>する地球の海面は、図d2のように変形して満干潮が発生します。
地球の月に面する部分の部分Dは最大の重力により月に向けて海面が盛り上がり満潮が発生します。
固体である地球はAよりも弱い中間程度の重力により月に引き付けられ、月から見て地球の裏側の部分Cの海水は地球本体より重力が弱いので、
地球から取り残された状態となり、地球から盛り上がり満潮となります。
AとBの海水は図d1(b)のA,Bに対応し、互いに引き寄せられるように海水が地球表面に張り付いて干潮が発生します。
このように、自由落下する局所慣性系内において重力の非局所的影響を生じさせることによる地球上の海面の満干潮現象現象が潮汐力と名付けた由来です。
<注> 地球と月との関係は、通常の感覚では、地球が静止しており、
月が静止した地球の周囲を旋回(公転)すなわち自由落下していると感じられます。
しかし、正確には、地球と月はその両者の合成重心位置を旋回中心にして地球も月もともに旋回(公転)しています。
そのようなわかりやすい例として陸上競技のハンマー投げでハンマーを回転することを考えてみます。
ハンマー投げ競技では、競技者は地面に対して直立したままではなく、
ハンマーと反対側に身体を傾けてハンマーを回転させます。
このようにハンマーの回転動作時は、競技者の足の地面の設置位置の鉛直線が回転中心(軸)となり、
競技者(の重心)とハンマー(の重心)の合成重心が回転中心軸上に存在することにより
競技者がバランスを崩さずに複数回の旋回ができることになります。
したがって、月も地球も互いに(自由)落下しながら回転しています。

図d1 潮汐力

図d2 満干潮
【コラム5】慣性質量と重力質量
\(x-y\)面が水平面、\(z\)軸が鉛直線(上方を正方向)とする静止座標系において
質点の落下運動を考えます(図e1)。
ニュートンの運動法則では、\(z\)方向の力\(F_{z}\)が作用する質点の\(z\)方向の運動方程式は次式により表されます。
\[
m_{I}\ \cfrac{d^{2}(t)}{dt^{2}} = F_{z} \tag{e1}
\]
ここで、\(m_{I}\)は質点に力が作用したときの質量の加速のされにくさを表すものとして定義されたものであり、
慣性質量と呼ばれています。
一方、重力場、例えば地球上では、質点に重力加速度が下向き(\(-z\)方向)に作用するため、
質点に作用する力\(F_{z}\)は次式で表されます。
\[
F_{z} = -m_{G}\cdot g \tag{e2}
\]
ここで、\(m_{G}\)は重力質量と呼ばれ、重力加速度が同一ならば強い重力が作用するものほど大きい質量であると定義されたものです。
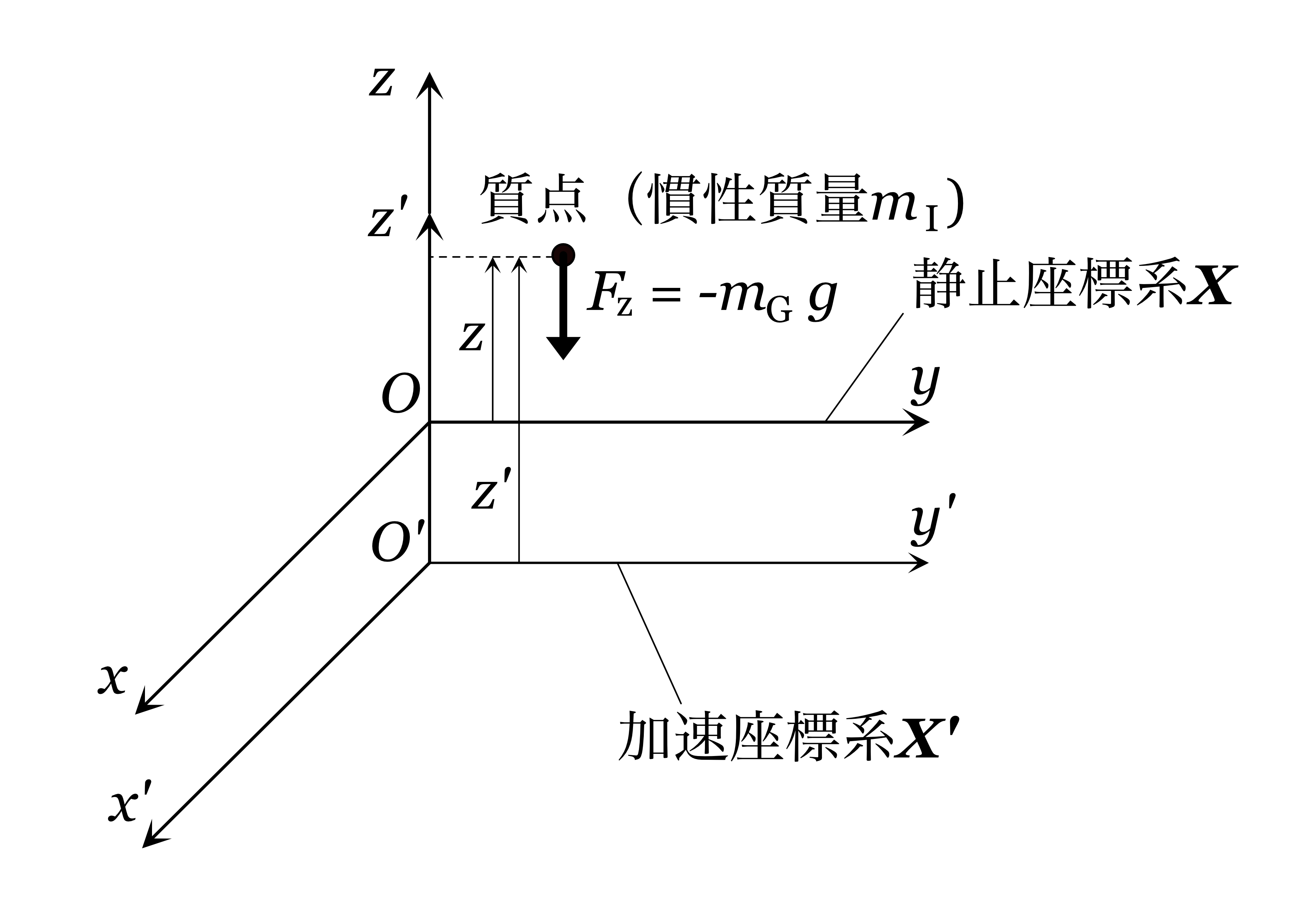
図e1 一様な重力場中の質点の自由落下
ところで、質点が重力場ではなく電場\(E\)に置かれ、質点の電荷が\(Z\)である場合には、質点に作用する力\(F_{z}=-ZE\)となるため、
(e2)式において電荷\(Z\)と電場\(E\)がそれぞれ重力質量\(m_{G}\)と重力加速度\(g\)に対応することになります。
そのため、電荷と慣性質量とは関係がないのと同様に重力質量と慣性質量とは本来、関係ないものとして定義されたものです。
(e1)、(e2)より、次式が得られます。
\[
\cfrac{d^{2}z(t)}{dt^{2}} = -\cfrac{m_{G}}{m_{I}}\cdot g \tag{e3}
\]
比電荷\(Z/m_{I}\)が粒子が異なれば異なるのと同様に、比\(m_{G}/m_{I}\)も粒子ごとに異なるはずですが、
現実の物理現象の観測から、重力質量と慣性質量は物質によらず正確に比例することが知られています。
そこで、この比例係数を1として重力質量を次式により定義することとしています。
このことは、逆に言えば、重力質量が慣性質量と同一になるように重力加速度\(g\)の値を定めているということができます。
\[
m_{G} = m_{I} \tag{e4}
\]
したがって、(e3)、(e4)より、質点の質量に関係なく次式が成立します。
\[
\cfrac{d^{2}z(t)}{dt^{2}} = -g \tag{e5}
\]
静止座標系\(\bm{X}\)(\(x, y, z\))に対して(e5)式による質点と運動(自由落下)と同じ運動(自由落下)する\(\bm{X'}\)座標系(\(x', y', z'\))を考えると、
座標変換式は次式で表すことができます。
\[
\begin{align}
x' &= x \notag \\
y' &= y \notag \\
z' &= z + \cfrac{1}{2}gt^{2} \notag \\
\end{align} \tag{e6}
\]
(e6)式第3式を2階微分して(e5)式を代入すると次式が得られます。
\[
\cfrac{d^{2}z'}{dt^{2}} = \cfrac{d^{2}z}{dt^{2}} + g = 0 \tag{e7}
\]
これより、運動座標系\(\bm{X'}\)から質点の運動を観測すると、
質点の加速度は0であり、重力加速度(すなわち重力)は消えており、\(\bm{X}'\)系は慣性系となっています。
\(\bm{X}'\)系は質点を内部に含み自由落下するエレベータに相当することから、
自由落下するエレベータ内は重力が消えていることの数学的説明となっています。
このように、重力場を座標変換により慣性系を形成することができるのは、
質点によらず重力質量が慣性質量に等しいからです。
そこで、あらゆる物質の重力質量と慣性質量が等しいことを等価原理と呼ぶこともあります。
3.2 地球上の高さによる時計の進行
天体の重力を受けない宇宙空間において加速する宇宙船の進行方向の後端と先端に設置した2つの時計A、Bの進み方を違いについて図4にて説明します。
先端の時計Bで1秒毎(周期\(\Delta T = 1sec\)、振動数\(\nu = 60Hz\))に先端から後端に向けて発光したパルス光を後端で受光して時計Aでの時間間隔(周期\(\Delta T_{0}\)、振動数\(\nu_{0}\))を計測して、
両者の時計の周期の相違について考えることとします。
宇宙船が位置\(z_{0}\)(速度\(v_{0}\))で先端の時計Bから第1のパルス光を宇宙船の後端の時計Aに向けて発光し、
宇宙船の後端の時計Aで受光したときの宇宙船の位置を\(z_{1}\)(速度\(v_{1}\))とします(図15(a))。
第1のパルス光発光の1秒後に、宇宙船が位置\(z_{2}\)(速度\(v_{2}\))で先端の時計Bから第2のパルス光を宇宙船の後端の時計Aに向けて照射し、
宇宙船の後端の時計Aで受光したときの宇宙船の位置を\(z_{3}\)(速度\(v_{3}\))とします(図15(b))。
このような測定を行うとき、後端の時計Aが第1のパルス光を受光するときの宇宙船の速度\(v_{1}\)より第2のパルス光を受光するときの宇宙船の速度\(v_{3}\)
の方が大きくなるので、\(L_{1} \gt L_{2}\) となります。
このため、後端の時計Aによる第1のパルス光から第2のパルス光の受光間隔(周期\(\Delta T_{0}\))は、先端の時計Bの発光間隔(周期\(\Delta T = 1sec\))より短くなります。
この現象は光のドップラー効果であるということができます。
速度\(v\) で近づく発光源(振動数 \(\nu_{0}\) )を受光する光の振動数νは次式で表されます。
\begin{equation}
\nu = \nu_{0}\cfrac{1+\cfrac{v}{c}}{\sqrt{1-(\cfrac{v}{c})^{2}}} \label{c1}
\end{equation}
ここで、時計Bからの発光が時計Aに到達する時間 \(t\) は \(t≒H/c\) であり、その時間\(t\)において宇宙船の速度\(v\)は \(gt = gH/c\) だけ増加します。
このため、時計Bから発光された瞬間に時計Aは \(v=gH/c\) の速度で近づいていくことになります。
したがって、\(v\) が \(c\) に対して十分小さいことを考慮すると、\eqref{c1}右辺の分母は1となり、\eqref{c1}から次式が導けます。
\begin{equation}
\nu = \nu_{0}\ (1 + \frac{gH}{c^{2}}\ ) \label{c2}
\end{equation}
パルス光の周期と振動薄は反比例するため、上式より次式が得られます。
\begin{equation}
\Delta T = \cfrac{\Delta T_{0}} {1 + \cfrac{gH}{c^{2}}\ } \label{c3}
\end{equation}
この結果、先端の時計Bの周期\(\Delta T\)(時計の進行の刻み)は後端の時計Aから観測された時計Bの周期\(\Delta T_{0}\)(時間の進行の刻み)より短く観測されるため、
後端の時計Aから観測すると、先端の時計Bの時間の進み方は早くなります。
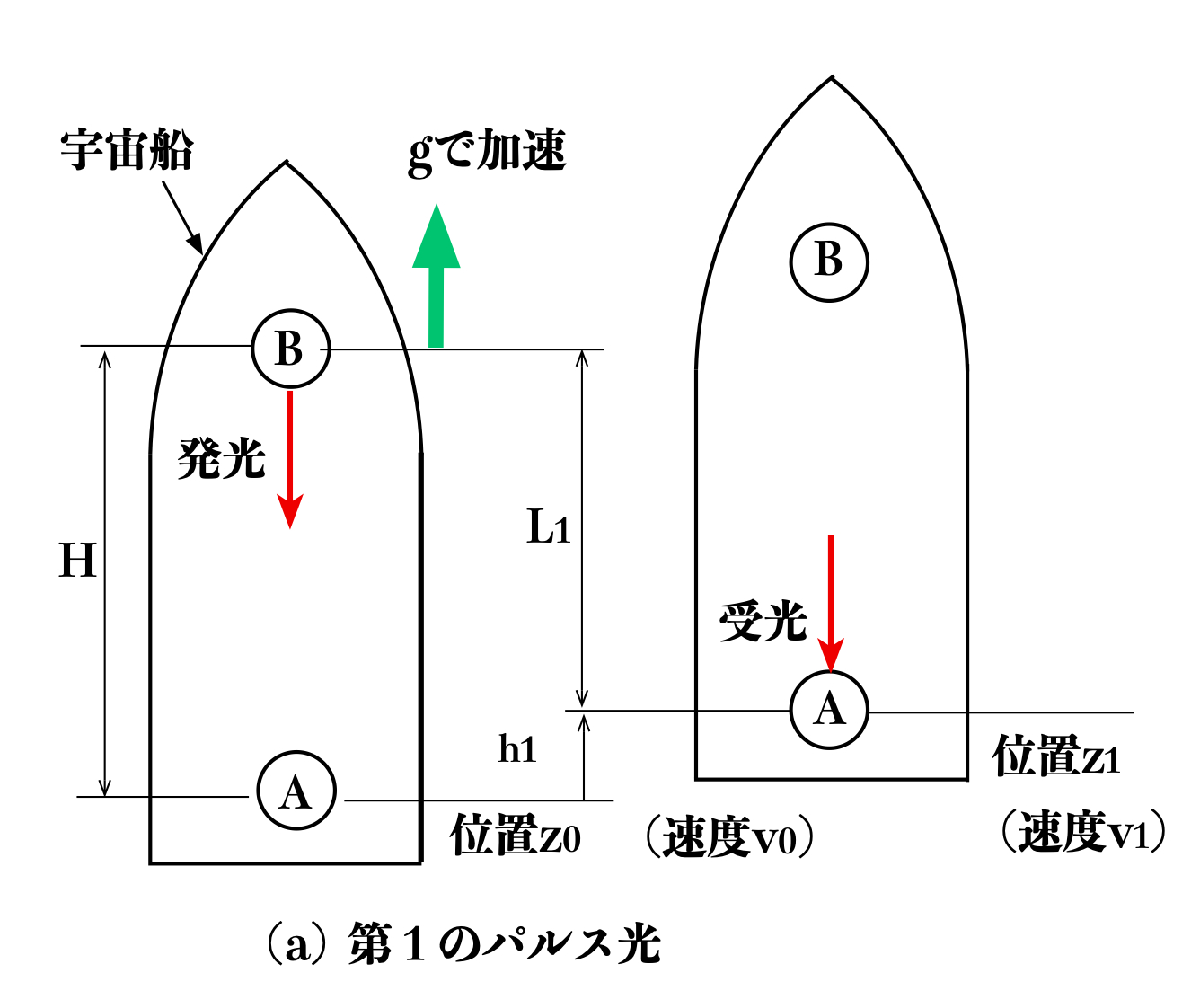
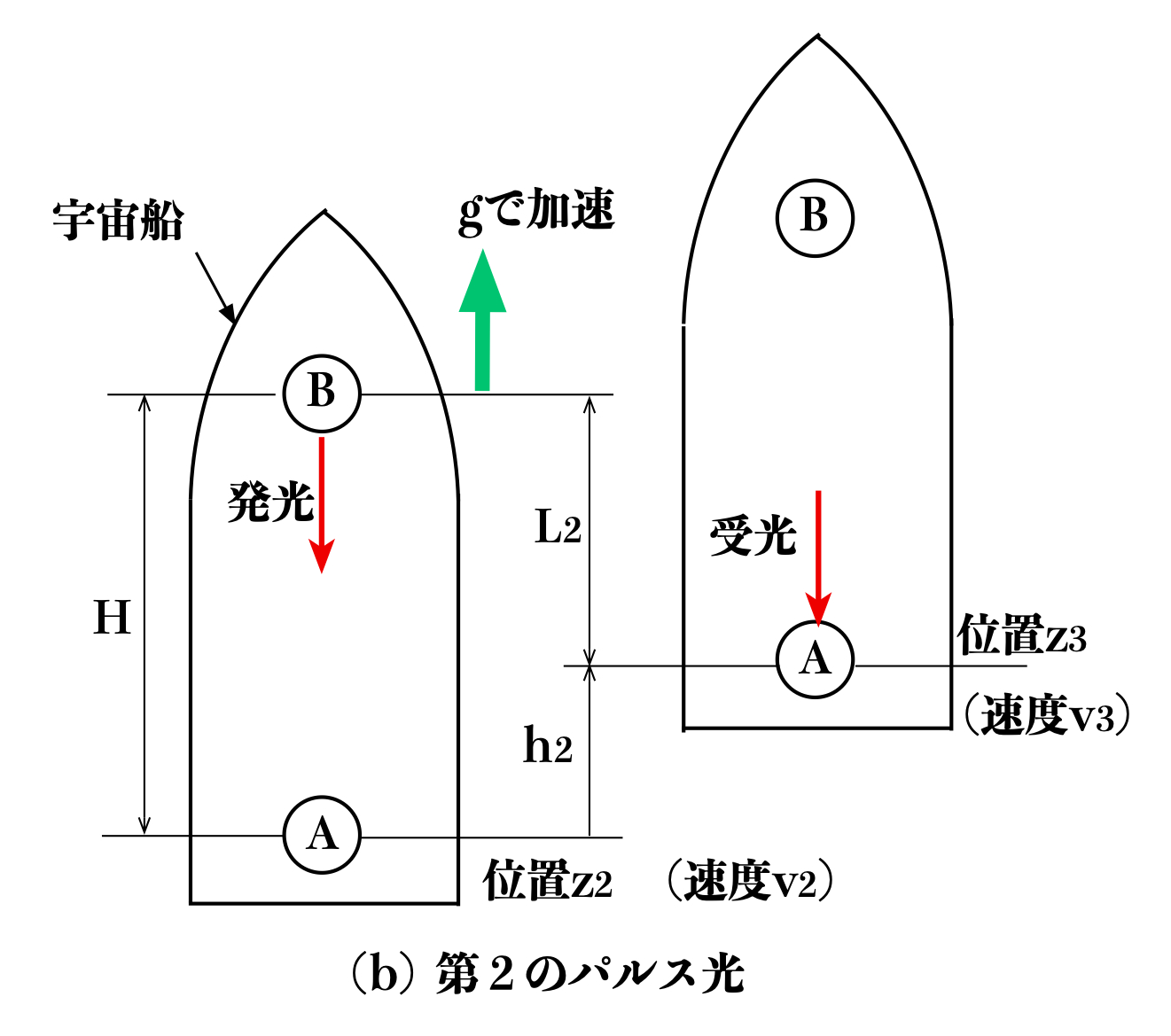
図4 重力を受けない宇宙空間で加速する宇宙船
上記については、等価原理により、宇宙船が加速上昇する代わりに重力の作用する地球上で静止している場合と同じとなります(1項参照)。
したがって、地上の床の時計Aから高所の時計Bを観測すると、高所の時計Bは床の時計Aよりも早く進んでいるように見えることとなります。
例えば、地表の高低差\(H\)=20mの振動数の差は上式より 2x10-15と非常に小さいですが、
メスバウアー効果(放射性物質の原子核から放射される特定振動数のγ線がエネルギーを失うことなく同種の原子核を含んだ吸収体に共鳴吸収される現象)
により発見されて確かめめられています。
3.3 時空の曲がり
”曲がった空間”の章で空間の曲がり、また前記”2.重力場の時計の遅れ”で重力場の高さにより時間の進行に相違があることについて説明しました。したがって、時間と空間が統合された時空としても曲がりがあることになります。
そこで、時空の曲がりについて、説明の便宜から、(\(t、x、z\))の3次元座標(水平面が時間軸\(t\)と空間\(x\)軸、縦軸が空間\(z\)軸)の図5に基づいて説明します。
地面高さのAと地上高さHのBとにおいた物体をともに、AとBそれぞれの時計で同一高さにおいて100秒移動させることとします。この場合、Aの時計から見ると、Bの時計の進行はAの時計の進行より早いので、A、Bそれぞれの物体の移動後のC、Dの時刻は同時ではなく、高さHにあるDの方が早く、両者の時刻は一致しません。
このため、重力場においては時空は曲がっています。
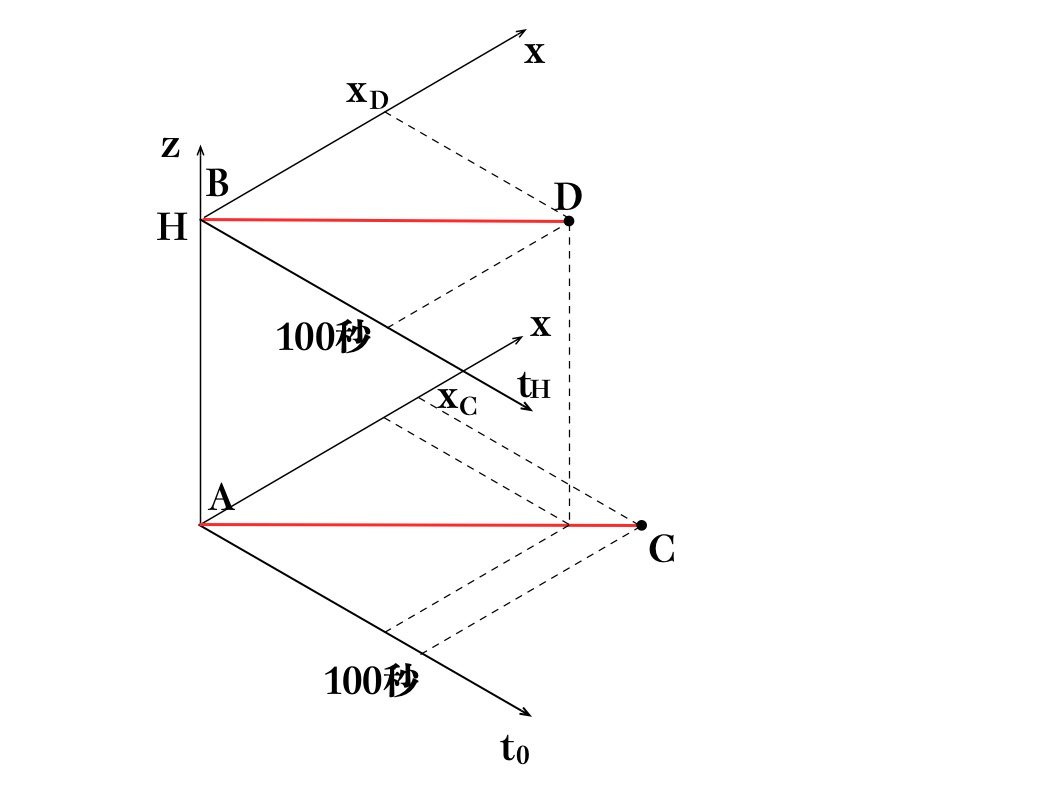
図5 重力場における時空の曲がり
【文献】
(1) 見城尚志、佐野茂:”幾何で見える必ずわかる一般相対性理論”、p.262、初版、2022年10月7日、株式会社技術評論社。
(2) 同上、p.284。