Ⅲ 基本原理から導かれる現象等
1.運動する物体の質量が増加する
静止しているときの質量\(m_{0}\)が速度\(v\)で動くとき、静止空間から見た質量\(m\)は増加するというものであり、
その質量は次式により求まります。
\begin{equation}
m= \frac{m_{0}}{\sqrt{1 - \beta \ ^{2}}} = \gamma \ m_{0} \label{1}
\end{equation}
ここで
\begin{align}
&\beta =\frac{v}{c} \label{2}\\
&\gamma = \frac{1}{ \sqrt{1-\beta \ ^{2}}} \label{3}
\end{align}
例えば、光速度\(c\) の90%の速度\(v\)(\( \beta = v/c=0.9\))で運動する物体は、\(m = 2.29m_{0}\) となり、質量が2.29倍に増加します。
\eqref{1}より、物体の速度\( v \) が大きくなり、光速度\( c \) に近づくにつれ、右辺分母のルート内の第2項が限りなく1に近づき分母が0に近づくため、
物体の質量\( m \)が無限大となり、加速が困難、不可能となります。
2.運動物体内の時間の進行が遅くなる
地面のような静止物体(静止座標系)から観測すると、一定速度\( v \)で運動する運動物体(運動座標系)に固定した時計の進行は、
静止座標系に固定した時計の進行より遅く観測されます。
この現象は、中学の数学(平面幾何)で習ったピタゴラス(三平方)の定理で導くことができますので、以下説明します。
図1のように2つのミラー(ミラー1及び2)の間を往復する光線の往復時間を基準として時間の進行を測定する光時計を考えます。
静止物体内に設置された光時計におけ光線のミラー間の1往復時間\( T \)をその静止物体において観測すると、
\( T \)は図1に示されるように次式で求まります。
\begin{align}
T = \cfrac{2d}{c} \label{4}
\end{align}
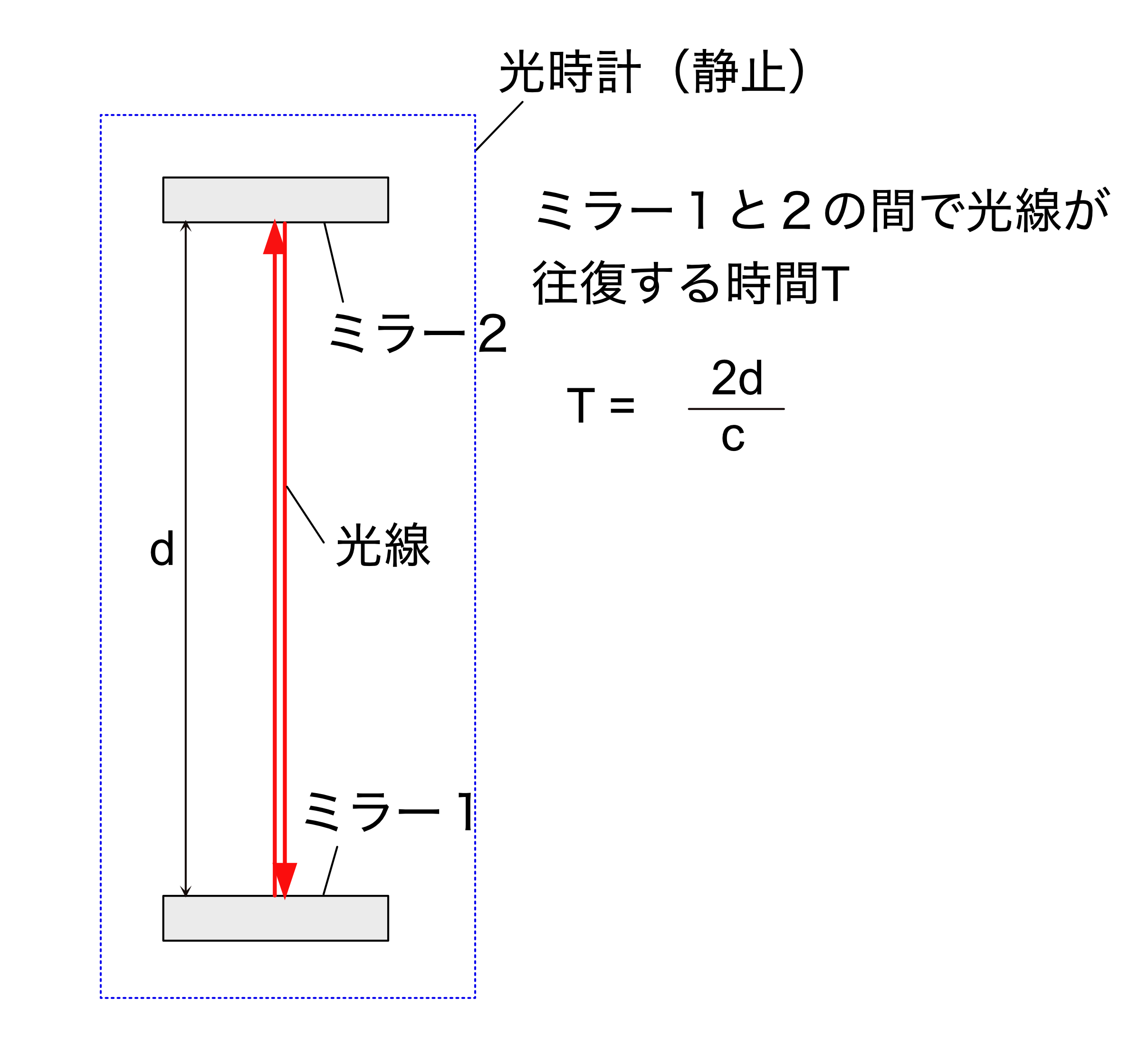
図1
これに対して、図2に示されるように速度\( v \)で運動する運動物体A内に設置した光時計を静止物体から観測したときのミラー間の光線の1往復時間を\( t \)とすると
ピタゴラスの定理より次式の関係が成立します。
\begin{align}
\Biggl( \cfrac{ct}{2} \Biggr)^{2} = d^{2} + \Biggl( \cfrac{vt}{2} \Biggr)^{2} \label{5}
\end{align}
\eqref{4}、\eqref{5}より、\(T\)と\(t\)との関係式は次式の通りとなります。
\begin{align}
T & = t \sqrt{ 1-(\cfrac{v}{c})^{2} \ } \notag \\
&= t \sqrt{ 1-β^{2} \ } \label{6}
\end{align}
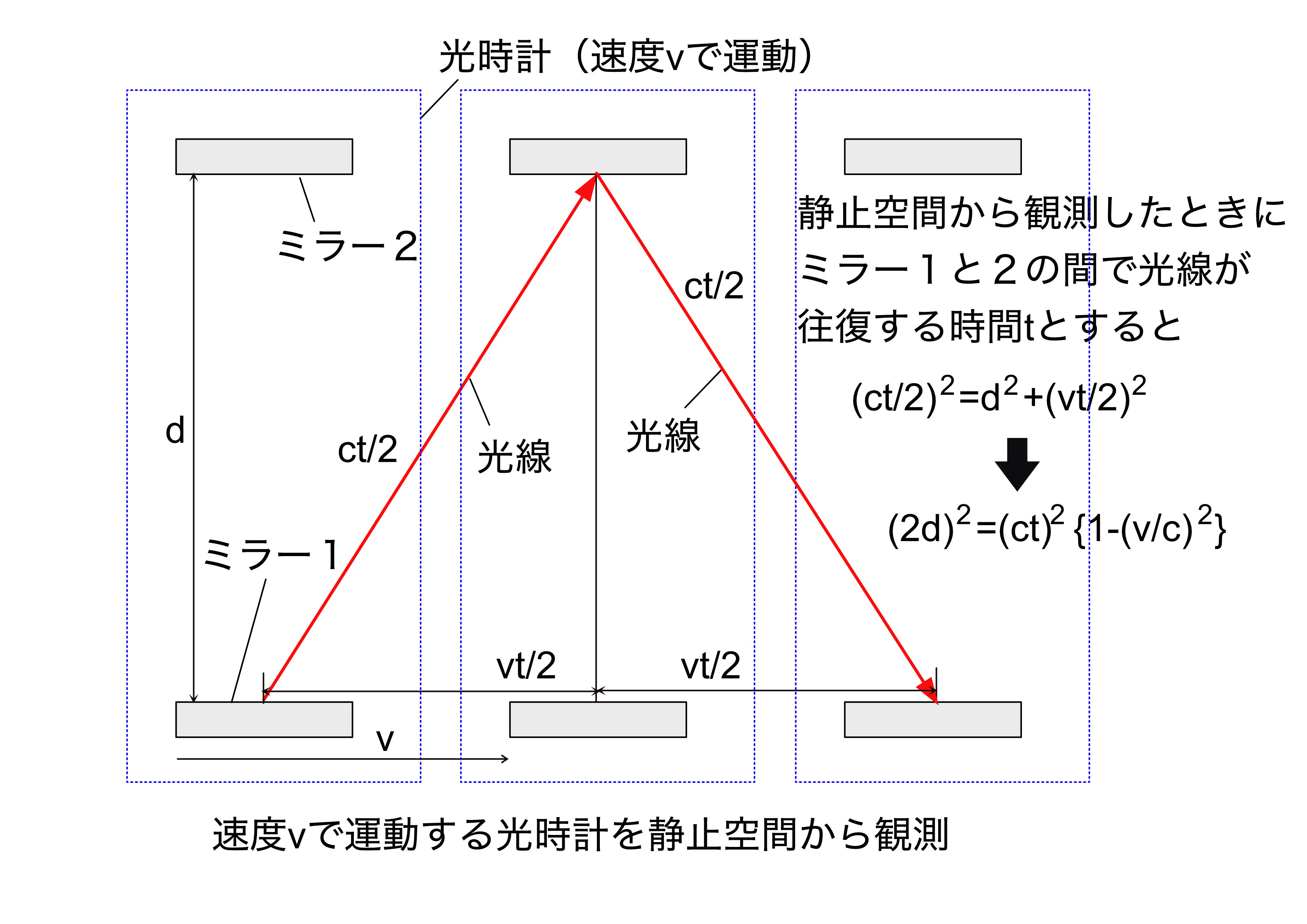
図2
\eqref{6}より、運動物体からは、運動物体内の経過時間\(T\)は静止物体内の経過時間\(t\)より短い、すなわち
運動物体の時間の進行は静止物体の時間の進行に比べて遅くなると観測されることになります。
例えば、光速に非常に近い速度\( v=0.9999c \)(光速\( c \)の99.99%)で移動する移動体に固定した時計の経過\(T\)は、
\eqref{6}より地面に固定した時計の時間の経過\(t\)に対して以下のように遅くなります。
\begin{align}
T &= t\sqrt{ 1 - \beta^{2} \ }\ = t\sqrt{ 1 - 0.9999^{2} \ } \notag \\
&= 0.01414\ t \label{7}
\end{align}
したがって、地球から観測すると移動体(宇宙船)内の時間の進行は非常にゆっくりとなります
(例えば、約1.4%のスピードで再生している動画を鑑賞しているように観測されます)。
この結果、地球に残った観測者は歳をとって行くの対して、高速で飛行する宇宙船で宇宙旅行している宇宙飛行士はほとんど歳を取らないように観測されます。
また、例えば、甲が乗った宇宙船が地球の近くから遠方の星に向けて速度\( v = 0.6c \)(\( β=0.6 \))で出発、飛行し、
宇宙船内の時計で10年後(\( T = 10 \ 年\))に甲が死亡した場合、
地球から観測した宇宙船内の経過時間\( t \)は、\eqref{6}により
\begin{align}
t &= \cfrac{T}{ \sqrt{ 1 - \beta^{2} \ } }\ = \cfrac{10}{ \sqrt{ 1 - 0.6^{2} \ } } \notag \\
&= 12.5\ (年) \label{8}
\end{align}
となるため、地球では、甲は地球から出発後12.5年間生存したものと記録されます。
なお、運動物体(運動座標系)内の時間の進行が遅く観測されるのは、静止物体(静止座標系)から静止物体内の時計の進行を基準とした観測によるものであって、
運動物体内の時計を基準とした時間の進行とは異なります。
すなわち、運動物体内でその運動物体内に設置された光時計の光線の1往復時間を観測すれば、静止物体内でその静止物体内の光線の1往復時間と同じ\eqref{4}による\( T \)となります。
そこで、静物物体、運動物体に限らず、その物体内に設置された時計に基づく経過時間を固有時間\( \tau \)といい、次式で表現されます。
\begin{align}
\tau = \cfrac{2d}{c} \lt t \tag{4a}
\end{align}
以上より、静止物体(静止座標系)から観測すれば運動座標系内は\eqref{6}で時間は進行しますが、
運動物体(運動座標系)内においては固有時間τにより時間は進行します。
【コラム2】高速で飛翔する素粒子の寿命
移動体内の時間の進行が静止体に固定した時計での時間の進行より遅くなる事例としてから宇宙線ミューオンの寿命(発生から消滅までの時間)を紹介します
(【文献】(1))。
宇宙線ミューオンは、大気に突入した1次宇宙線(陽子やアルファ粒子)が地上から数kmないし10km程度の上空の大気中の原子や分子に衝突して発生し、
光速に近い速度\(v = 0.99c\)で地上に向けて降り注ぎます。
ミューオンの平均寿命は\( \ 2.2 \x 10^{-6} \)秒と非常に短いため、ニュートン力学によれば、宇宙線ミューオンの飛行距離は
\(
0.99 \x 3.00\x 10^{5}\mathrm{(km/s)} \x 2.2\x10^{-6}\ \mathrm{(s)} = 0.653\ \mathrm{km}
\)
となり非常に短く、地上に到達するまでの大気中で消滅するはずですが、現実には地上まで到達して観測できています。
上空で発生した宇宙線ミューオンが地上で観測できるのは、光速に近い速度で運動する宇宙線ミューオンに固定した時計の進行(発生から消滅までの時間)が
地上で観測されたミューオンの消滅までの時間より遅くなるためです。
具体的に検討します。宇宙線ミューオンの速度\(v=0.99c\)、平均寿命\( \tau_{m} = 2.2x10^{-6} \)(s) を\eqref{4}に代入すると、
地上から観測された宇宙ミューオンの平均寿命\(T_{m}\)は、
\( T_{m} = \cfrac{τ_{m}}{\sqrt{ 1-β\ ^{2} \ } \ }\ = \cfrac{2.2\times 10^{-6}}{\sqrt{ 1-0.99\ ^{2} \ } \ } \)
\( = 15.6\x 10^{-6}\ \mathrm{(s)}\)
となり、地上で観測された宇宙線ミューオンの平均寿命は長くなります。
したがって、地上から観測すると、宇宙線ミューオンの平均寿命に対する飛行距離は、
\(
0.99\x 3.00\x10^{5}\mathrm{(km/s)} \x 15.6\x10^{-6}\mathrm{(s)} = 4.63\ \mathrm{km}
\)
と非常に長くなり、多くの宇宙線ミューオンが地上に到達することができます。
3.運動物体は運動方向の長さが収縮する
地面に対して一定速度\(v\)で運動する物体の長さは運動方向に収縮するという現象(ローレンツ収縮)です。
長さ\(L_{0}\)の棒が地面に対して速度\(v\)で動くときは、地面から観測された棒の長さ\(L\)は次式の長さになります。
\begin{equation}
L= L_{0}\ \sqrt{1-β\ ^{2}}\ =\frac{\ L_{0}\ }{γ\ }\label{9}
\end{equation}
例えば、光速度\(c\)の90%の速度\(v(v/c=0.9)\)で運動する物体は、\(L=0.436L_{0}\)となり、長さが44%に収縮します。
\eqref{9}より、物体の速度\(v\)が大きくなり、光速\(c\) に近づくにつれ、右辺の平方根(ルート)内の\(β^{2}\)が1に近くなり右辺が0に近づくため、
運動方向の長さ\(L\)が0に近づいていきます。
【コラム3】高速で飛翔する宇宙線ミューオンから観測された大気の厚さ
コラム2で検討した宇宙線ミューオンが飛翔できる大気厚さについては、ローレンツ収縮の観点からも計算することができます。
亜光速で飛翔する宇宙線ミューオンを基準(静止)とする慣性系とすれば、大気を含む地球は\(-0.99c\)の速度で運動する移動体とみなすことができます。
したがって、例えば大気の厚さ\(L_{0}\)=5kmは、亜光速\(v=0.99c\)で飛翔する宇宙線ミューオンから観測すると、\eqref{5}より、
\[
L = 5000\ \sqrt{1-0.99\ ^{2}}\ = 705\ \mathrm{(m)}
\]
であり、この大気の厚さを通過して地上に到達するまでの宇宙船ミューオン固定の時計による経過時間τは、
\(
τ = \cfrac{L}{0.99c} = \cfrac{705\mathrm{(m)}}{0.99\x 3.00\x 10^{8}\mathrm{(m/s)}}= 2.37\x 10^{-6}\ \mathrm{(s)}
\)
となるため、ミューオンの平均寿命\(2.2\x10^{-6}\ \mathrm{(s)}\) とほぼ同じとなります。
これにより、亜光速で飛翔する宇宙線ミューオン固定の時計によれば、宇宙線ミューオンの多くが寿命による消滅前に地上に到達することができます。
4.同時であることの相対性
次の例題を考えてください。
【例題3】
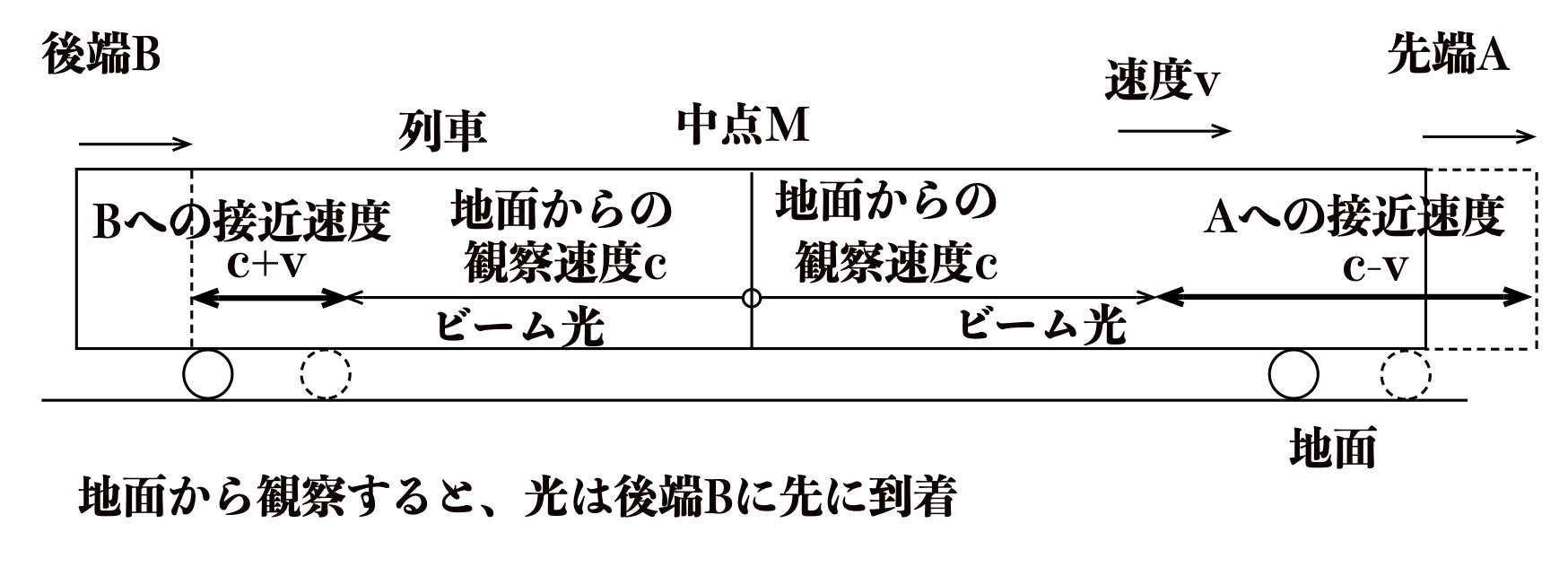
速度\(v\)で走行する列車の中で先端Aと後端Bとの中点Mから先端Aと後端Bに向けて同時にビーム光を投光した。
列車内及び地面から観測した場合のビーム光のA、Bへの先後について答えてください。
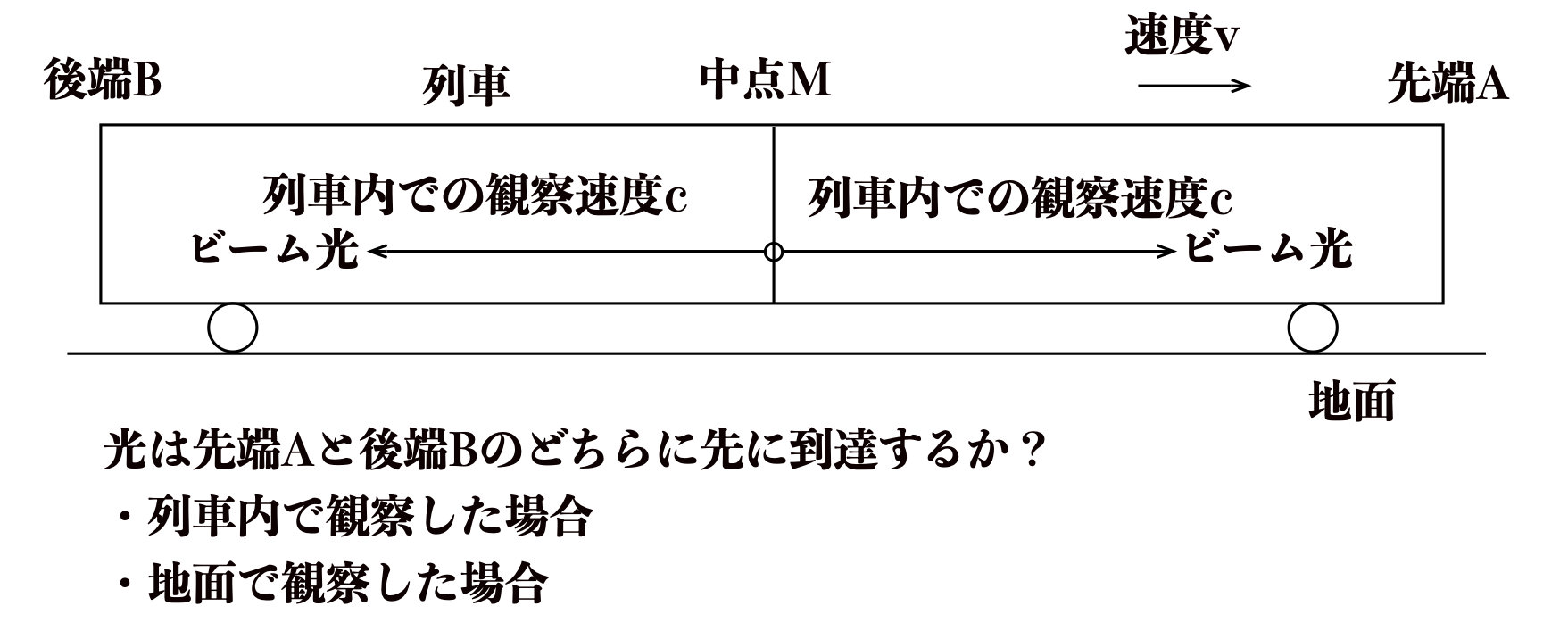
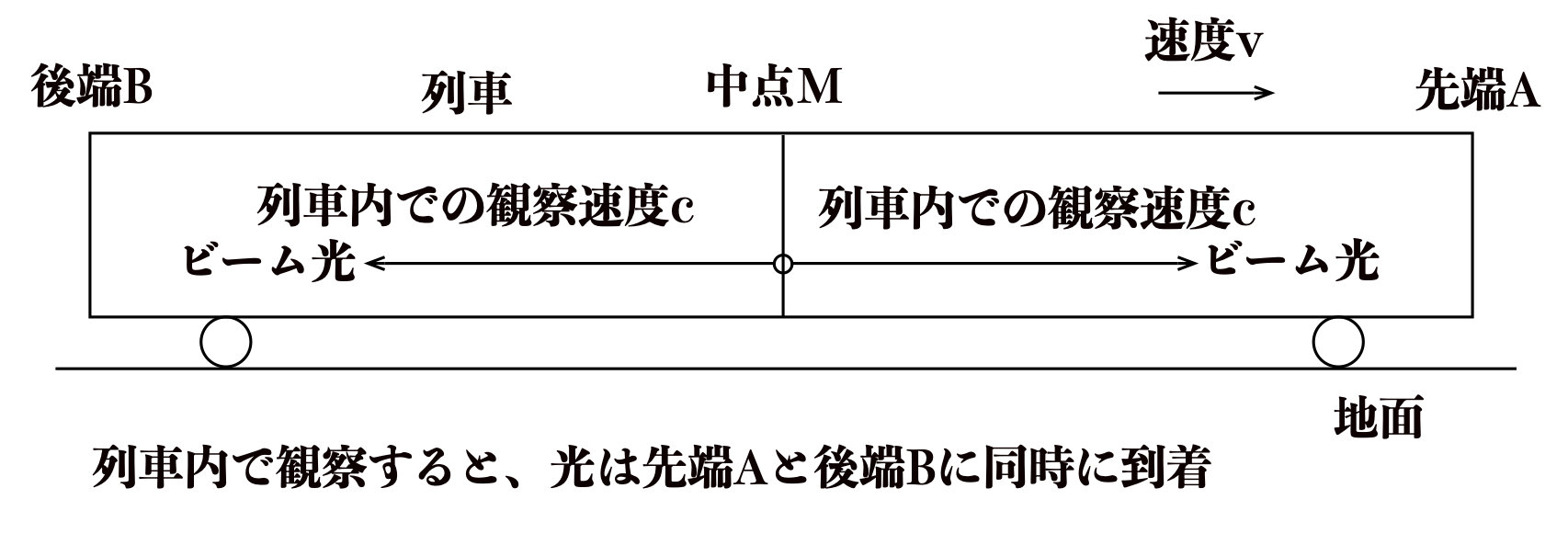
【例題3の解答】
列車内で観測すれば、等距離にあるMA間とMB間を光速度\(c\) で進むので同時に到着するが、
地面から観測すれば後端Bに先に到着します。
その理由は以下の通りです。
地面から観測すると、先端Aに向かう光速も後端Bに向かう光速も同じ\(c\) です(例題2の解答参照)。
したがって、地面から観測すると、先端Aに向かう光と先端Aとの接近速度は\(c-v\)(先端Aはビーム光から逃げるように動く)であるのに対して、
後端Bに向かう光と後端Bとの接近毒度は\(c+v\)(後端Bはビーム光に近づくように動く)となるため、ビーム光は後端Bに先に到着します。
このように、列車内で観測すると同時刻に発生した事象が、地面からは同時刻ではなく異なる時刻に発生したと観測されます。
これを同時刻の相対性と呼び、同時性については観測系の間では絶対的なものではなく、相対的なものとなります。
5.質量とエネルギーは等価である
静止質量\(m_{0}\)の物体は、次式で表されるものとエネルギー\(E_{0}\)と等価であり、
質量とエネルギーとが相互に変換することができます。
\begin{equation}
E_{0}= m_{0}\ c^{\ 2} \label{10}
\end{equation}
したがって、例えば、物体の質量が消失し、その消失した質量がエネルギーに変換されます。
ただし、日常生活を初めてとして通常の場合には、質量が消失してこエネルギーが放出されることはありません。
このエネルギーが放出されるのは、核反応等により原子等の質量の一部が欠損し、その欠損質量がエネルギーに変換した場合になります。
例えば、原爆の爆発、原子力発電所(原子炉)の熱源としての利用の場合です。
また、自然界では、太陽は水素原子核4個の核融合によりヘリウム原子核が生成されているところ、
水素原子核4個の合計質量よりヘリウム原子核1個の質量が少し小さいため、その質量差がエネルギーに変換されています。
6.物体の運動速度には上限がある
\eqref{1}等において、右辺のルート内は正でなければならないので、\(v\lt c\ \)すなわち物体の運動速度\(v\)は光速度\(c\)より小さくなります。
なお、現在、宇宙の非常に遠方の天体(銀河等)が光速度\(c\)以上の速度で地球からの距離が離れていくことが観測されています。
しかし、これは天体の物体としての運動速度ではなく、宇宙空間の性質として(風船の膨張のように)宇宙が空間として膨張しているものと考えられています。
宇宙が空間として均質に膨張すれば、地球から近い天体に比べて遠い天体はその距離に比例して離れる速度が大きくなり、
所定の距離以上に離れると離れる速度は光速を超えることになります。
したがって、光速を超えて地球から離れていく天体からの光については、地球に届かないことになるため、その天体の観測はできないことになります。
ただし、その天体が光速を超えて離れる前に発した光については、地球の届くため観測できることになります。
【コラム4】速度の合成
静止空間(慣性系K)に対して一定速度\(v\)で運動している空間(慣性系K’)の内部において速度\(v_{1}\)で運動している粒子を静止空間から観測すると、
特殊相対性理論では、粒子の速度\(v_{2}\)は次式となります。
これを速度の合成または速度の加算法則といいます。
\[
v_{2} = \cfrac{v+v_{1}}{1+\cfrac{vv_{1}}{c^{2}}}
\]
上式より、\(v=v_{1}=c\)とすると、\(v_{2}=c\)となり、静止空間から観測された粒子の速度\(v_{2}\)が光速\(c\)を超えることはありません。
一方、この速度の合成を【例題1】に適用すると、\(v\)=列車の速度、\(v_{1}\)=列車内での銃弾の速度、\(v_{2}\)=地面で観測した銃弾の速度となります。
上式において、\(v\)、\(v_{1}\)ともに光速度\(c\)に比べて非常に小さいので、
\[
v_{2} \simeq v+v_{1}
\]
となり、ニュートン力学で解いた【例題1の解答】の結果と一致します。
このことから、特殊相対性理論は、ニュートン力学も包含していますが、
工学、通常の物理現象その他の分野では複雑な特殊相対性理論によらずニュートン力学が実用的です。
【文献】
(1) Richard P. Feynman、Robet B. Leighton、Matthew Sands:”The Feynman Lectures on PHYSICS Mainly Mechanics, Radiation, and Heat”, p.15-7, Fourth Printing 1969, Addison-Wesley Publishing Company.