Ⅱ 基本原理
特殊相対性理論は、簡単に言えば、静止した空間(例えば、地面)と一定速度で運動する空間(例えば、列車やロケット等の内部空間)における物理現象に関する理論です。
地球は太陽の周りを公転しているので、太陽を基準とすれば静止していませんが、地面と列車との関係でいえば、地面は静止しているとみなすことができます。
逆に、列車を静止していると考えれば、地面は列車に対して一定速度で運動しているとみなすこともできます、通常の場合は、地面を静止空間と考えることとしています。
静止空間、一定速度で運動している空間のことを一般に「慣性系」と呼んでいます。
先ず、次の例題を考えてみましょう。
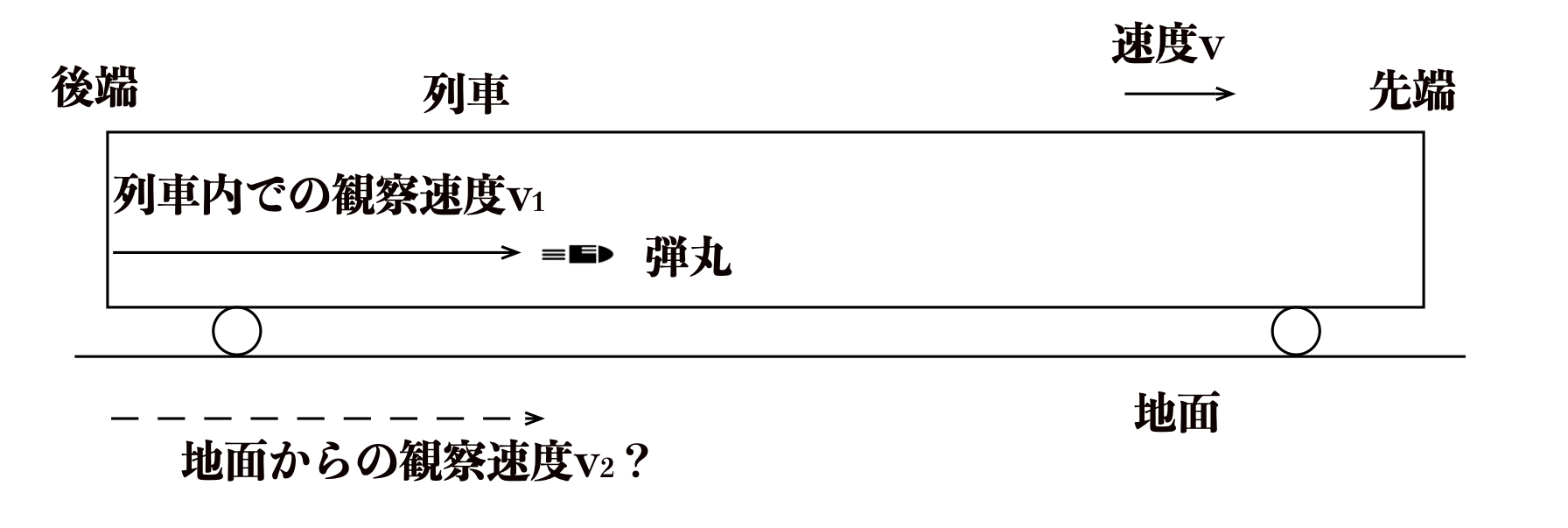
【例題1】
速度\(v\)で走行する列車の後端から先端に向けて銃弾を発射した。
列車内で観測された銃弾の速度が\(v_{1}\)であったとき、
地面から観測された銃弾の速度\(v_{2}\)を求めなさい。
なお、空気抵抗による減速、重力による落下等を考えないものとします。
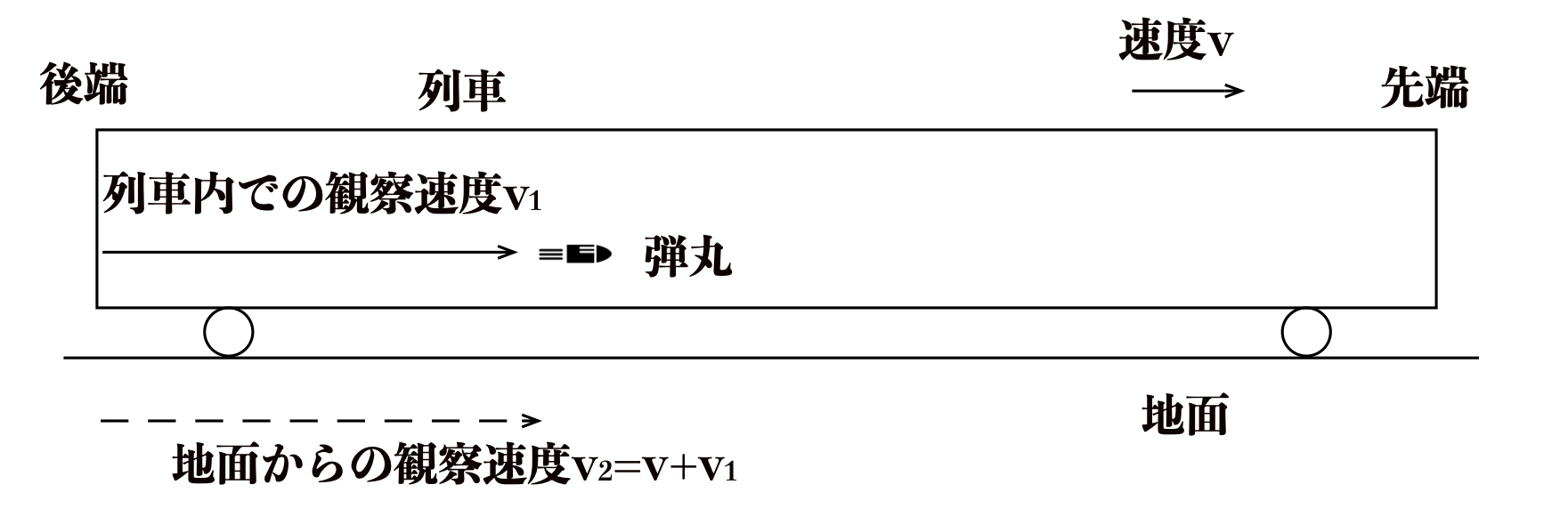
【例題1の解答】
地面で観測した銃弾の速度\(v_{2}\)は、\(v+v_{1}\)となります。
地面から観測すると銃弾を装填した拳銃は列車の速度と同じ\(v\)で運動しているため、
地面から観測された銃弾の速度は\(v_{2}\)は、列車内で観測された銃弾の速度\(v_{1}\)が加算されるためです。
次に、例題1において、「銃弾」を「光」に置き換えた次の例題を考えてみましょう。
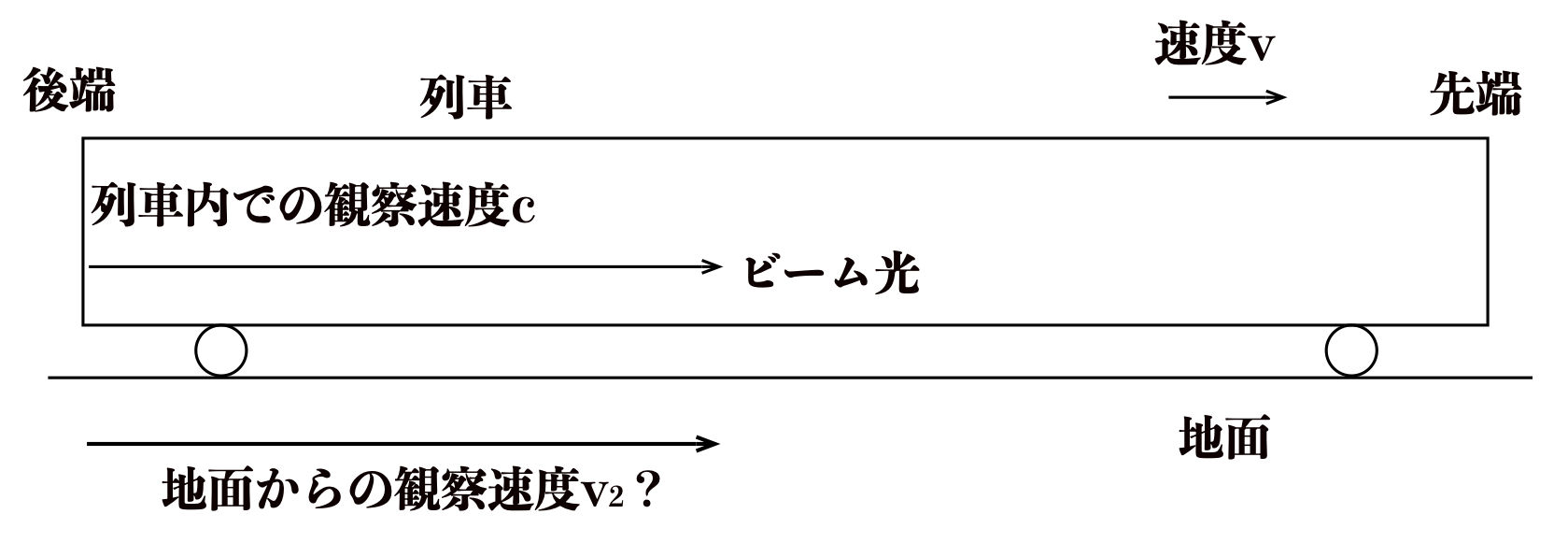
【例題2】
速度\(v\)で走行する列車の後端に設置したビーム光照射源から先端に向けてビーム光を照射した。
列車内で観測されたビーム光の速度(光速度)が\(c\)であったとき、
地面から観測されたビーム光の速度\(v_{2}\)を求めなさい。
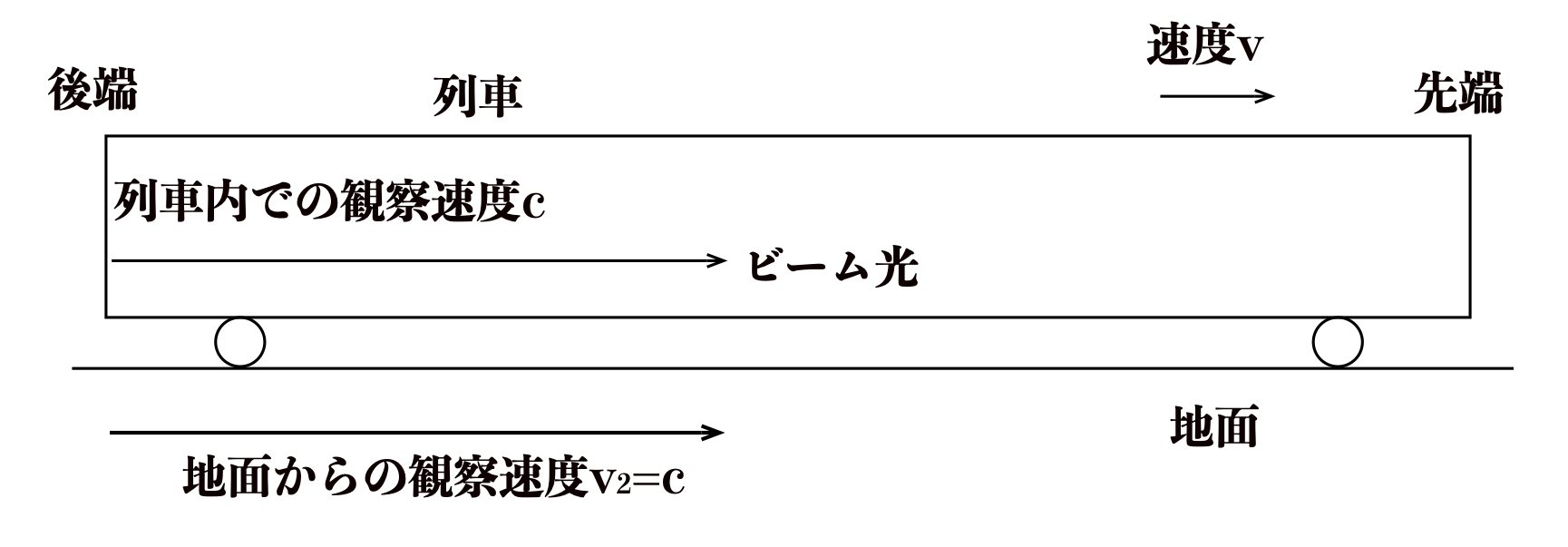
【例題2の解答】
地面から観測されたビーム光の速度\(v_{2}\)は列車内で観測された速度と同じ\(c\)です。
解説
例題1と例題2の解答は異なります。
例題1と例題2には、どのような相違があるのでしょうか?
例題1が銃弾という物体の運動に関する現象であるのに対して、例題2は光の運動に関する現象であり、例題1は従来のニュートン力学で解き、
例題2は特殊相対性理論で解いています。
私たちの通常の生活、天体の運行等における物体の運動に関しては、19世紀頃までは、従来の力学、いわゆるニュートン力学で説明、理解、解明ができます。
しかし、科学の発展に伴い、電磁気現象等においてニュートン力学で説明や解明できない場合があることがわかってきました。
ちなみに、光は電磁波の一種です。
このような状況下、それらの現象を解明するためにアインシュタインにより提案されたのが相対性理論であり、
先ず初めに、特殊相対性理論が発表されました。
特殊相対性理論の中心となるのが、以下の光速度不変の原理です。
光速度不変の原理
光の速度(光速度)はどの観測系から見ても一定(不変)である。
したがって、地面から観測された光速度は、列車内で観測された光速度と同じとなります(例題2)。
ちなみに、真空中の光速度\(c_{0}\)は3.00x105km/sです(コラム1参照)。
【コラム1】光速c
光は電磁波の一種です。電磁波の波動方程式より真空中の光速度\(c_{0}\)を理論的に求めると
\[
c_{0}=\frac{1}{\sqrt{ε_{0}μ_{0}}}
\]
となり、物性値である透磁率\(ε_{0}\)(8.957x10-12 F/m)と誘電率\(μ_{0}\)(1.257x10-6 H/m)のみで定まります
(詳細は第2部補説(もう一歩先へ)Ⅰ(光とは)の"3.電磁波の方程式"参照)。
このことは、従来のニュートン力学における理解と反することになります。ニュートン力学では、速度は基準(例えば、静止状態にある座標系)等があってそれを基準にして特定できるものです。
例えば、例題1においての列車内での銃弾速度\(v_{1}\)は列車内での静止物を基準としたものであり、地面からの観測速度\(v_{2}\)は静止空間の静止物(例えばレール)を基準としたものです。
したがって、上記式により、光速に関しては、ニュートン力学に反して、観測する空間(慣性系)や基準等に関係なく定まることが理論的にも示されています。
また、光速度不変の原理は、1887年に行われたマイケルソンーモーレイによる実験によっても実証されています。