Ⅴ 光とは
光は、相対性理論において特に重要な概念ですので、改めて説明します。
1.光の種類
光は広義には電磁波をいいますが、狭義には電磁波のうち人間の視覚で認識できる波長(380nm〜760nm)である”可視光線”をいいます。
電磁波は主として波長により表1のとおり分類されており、
プランク定数\(h=6.6253 \x 10^{-24} \ \mathrm{J} \cdot \mathrm{sec} \)、周波数\( \nu \)とすると、
電磁波のエネルギー\(E\)は
\begin{equation}
E = h \nu \label{1-1-1}
\end{equation}
であるから、周波数の高い電磁波ほどエネルギーが大きく、また透過力が大きいため、人間や動物に障害を発生させ、
また無生物等にも影響を与えるることになります。
このため、特に周波数の高いγ線とX線は、放射線として法律等により取り扱い等が厳しく規制されています。
赤外線より周波数の低い(波長の長い)電磁波は一般に電波と呼ばれています。
相対性理論における説明においては、特に断らない限り「光」は電磁波をいうものとします。
| 放射線 | γ線 | 3x1016Hz以上 | 10nm以下 |
| X線 | |||
| 紫外線 | 3x1015〜16Hz | 10〜380nm | |
| 可視光線 | 3x1013〜15Hz | 380〜760nm | |
| 赤外線 | 3x1012〜13Hz | 0.76〜1,000μm | |
| 電波 | サブミリ波 | 3x1011〜12Hz | 0.1〜1mm |
| マイクロ波 | 3x108〜11Hz | 1mm〜1m | |
| 超短波 | 3x107〜8Hz | 1〜10m | |
| 短波 | 3x106〜7Hz | 10〜100m | |
| 中波 | 3x105〜6Hz | 0.1〜1km | |
| 長波 | 3x104〜5Hz | 1〜10km | |
| 超長波 | 3x103〜4Hz | 10〜100km | |
| 極超長波 | 3x102〜3Hz | 100〜1,000km | |
| 極低周波 | 1〜300Hz | 1,000km以上 | |
2.光の発生メカニズム
太陽、高熱物体、電球から放出される光(電磁波)を発生メカニズムについて説明します。
物質を構成する原子は、一般に、陽子(正電荷)と中性子(中性)から構成される原子核および陽子と同数の電子(負電荷)から構成され、
電子は原子核の周囲を軌道を描いて回転しています。
原子核の周囲を回転する電子は、電子の保有エネルギーにより不連続な複数のエネルギーレベルの軌道を取ることができます。
安定状態の原子では電子は最も低い軌道上を回転しますが、電子が外部より所定のエネルギーを得ることにより、
エネルギー的に高い軌道に移ります。このように電子が高いエネルギーになった状態を励起状態といいます。
なお、外部から供給されるエネルギーが電子の最大励起軌道より遥かに大きい場合は、電子は原子の外に飛び出します
(所定以上のエネルギーを持つ光を金属の表面に照射したときにその金属の表面から電子が飛び出す現象を「光電効果」といいます(後記3②参照))。
このような状態の状態の原子は、原子全体として正電荷となるので、電離といいます。
ここで、例えばエネルギー\( E_{H} \)に励起状態にある電子がエネルギー\( E_{L} \)の安定状態へ変化(遷移)すると、
そのエネルギーの差\( \Delta E = E_{H} - E_{L} \)のエネルギーを持つ光(電磁波)が放出されます。
\( \Delta E = E_{H} - E_{L} \)のエネルギーを持つ光の周波数νは\eqref{1-1-}より算出されるので、
発生した光の波長λは
\begin{equation}
\lambda = \cfrac{hc}{\Delta E} \label{1-1-2}
\end{equation}
となります。
3.光の性質と論争
光は表2に示されるような基本的性質を持っています。
| 直進 | 光は均質媒質中では直進する。 |
| 反射・屈折 | 光は異なる媒質の境界面でが反射又は屈折する。 |
| 通過・吸収 | 光が透明な媒質の内部を通過するときは、その通過する媒質内で光が吸収される。 |
| 干渉 | 位相差が時間とともに変化しない同一周波数の2つの光波が重なり合うことにより強め合い又は弱め合う(干渉する)。 |
| 回折 | 光が伝搬するときに障害物の背後の回り込むこと(回折)ができる。 |
これらの光の性質のうち、例えば干渉や回折は光が波動でなければ起こり得ない現象であるため、古くから光は波動であると考えられていました。
しかし、ニュートンの古典物理学の時代には、波動は媒質(水面波の水、音波の空気、圧力波の固体等)の存在が前提となるため、
真空の宇宙空間を光波の伝搬を説明するために宇宙空間に「エーテル」が充満しているとして説明していましたが、
19世紀末頃までにエーテルの存在を実証できるような現象が見つかりませんでした。
また、19世紀末頃までに以下のような光の粒子性を示す現象が発見されていたため、
光が波動なのか粒子なのかが物理学において議論となっていました。
①日焼け現象
光が波であるとすれば、光のエネルギーは光波の振幅の2乗に比例することになるため、
太陽光からの紫外線と同程度の強さのエネルギーの可視光を照射できる電球を準備して人体に照射すれば、
日焼けができるはずですが、そのような電球により日焼けは起こりませんでした。
一方、光が粒子であり、波長又は振動数に対応したエネルギーを持っていると考えれば、
可視光ではなく紫外線で照射しなければ日焼けが発生しないことが説明できます。
具体的には、周波数νの光は\(h\)νのエネルギー(\(h\)=プランク定数6.626x10-34J•s)を持っており、
紫外線の周波数は可視光線の周波数より2桁程度大きいため、光線のエネルギーの相違も同様です。
②光電効果
光電効果は、1887年に電磁波の実験中にヘルツによって発見された現象であり、
金属板表面に周波数νの光を照射すると、その照射光の周波数νが金属ごとに特定の周波数ν0より大きければ、
金属板が光を吸収して電子(「光電子」という。)を放出するが、νがν0より小さければ照射光の強さを高めても
光電子を放出しないというものです。
アインシュタインは、特殊相対性理論の論文を発表した1905年に、
この光電効果に関して光の粒子性を論証した「光量子仮説」としての論文発表を行い、
(特殊相対性理論ではなく)この論文によりノーベル賞を受賞しています。
4.電磁波の方程式
19世紀、電磁気学の発展により電磁場理論が整備され、電磁波の方程式、光速cが理論的に導かれました。
(1)Maxwellの方程式
\(\bm{E}\)、\(\bm{D}\)、\(\bm{H}\)、\(\bm{B}\)をそれぞれ、電場の強さ(電界強度)、電束密度、磁場の強さ(磁界強度)、磁束密度とし、 \(ε_{0}\)、\(μ_{0}\)をそれぞれ真空の誘電率、透磁率とすると、次の関係式が成り立ちます。 \begin{equation} \bm{D} = ε_{0} \bm{E} \label{1-1} \end{equation} \begin{equation} \bm{B} = μ_{0} \bm{H} \label{1-2} \end{equation} また、\(ρ\)、\(σ\)、\(\bm{j}\)(\(=σ\bm{E}\))をそれぞれ電荷密度、導電率、電流密度とすると、 次の4つの方程式を合わせたマクスウエルの方程式が成立します。
【誘電体内におけるガウスの定理】 \begin{equation} \mathrm{div} \bm{D} = ρ \label{1-3} \end{equation} 【真磁価の不存在】 \begin{equation} \mathrm{div} \bm{B} = 0 \label{1-4} \end{equation} 【ファラデーの電磁誘導の法則】 \begin{equation} \mathrm{rot} \bm{E} = -\dd{\bm{B}}{t} \label{1-5} \end{equation} 【拡張されたアンペールの法則】 \begin{equation} \mathrm{rot} \bm{H} = \bm{j} + \dd{\bm{D}}{t} \label{1-6} \end{equation}
【ベクトルの微分】
\(x\)軸、\(y\)軸、\(z\)軸方向の単位ベクトルをそれぞれ\(\bm{e_{x}}\)、 \(\bm{e_{y}}\)、\(\bm{e_{z}}\)とします。
ベクトルのスカラーでの微分
\(
\cfrac{\partial \bm{B}}{\partial t} = \bm{e_{x}}\cfrac{\partial B_{x}}{\partial t} + \bm{e_{y}}\cfrac{\partial B_{y}}{\partial t}
+ \bm{e_{z}}\cfrac{\partial B_{z}}{\partial t}
\)
発散
\(
\mathrm{div} \bm{D} = \cfrac{\partial D_{x}}{\partial x} + \cfrac{\partial D_{y}}{\partial y} + \cfrac{\partial D_{z}}{\partial z}
\)
回転
\(
\mathrm{rot} \bm{E} =
\begin{vmatrix}
\bm{e_{x}} & \bm{e_{y}} & \bm{e_{z}}\\
\cfrac{\partial}{\partial x} & \cfrac{\partial}{\partial y} & \cfrac{\partial}{\partial z}\\
E_{x} & E_{y} & E_{z}
\end{vmatrix}
\)
(2)電磁波の方程式の導出
電荷が存在せず(\(ρ=0\))、絶縁物(\(σ=0\))である真空空間において、
時間的に変化する電場\(\bm{B}\)と磁場\(\bm{B}\)が存在すると仮定し、
\eqref{1-1}と\eqref{1-2}を考慮するとマクスウエルの方程式は次式となります。
【誘電体内におけるガウスの定理】 \begin{equation} \mathrm{div} \bm{E} = 0 \label{1-7} \end{equation} 【真磁価の不存在】 \begin{equation} \mathrm{div} \bm{B} = 0 \label{1-8} \end{equation} 【ファラデーの電磁誘導の法則】 \begin{equation} \mathrm{rot} \bm{E} = -μ_{0}\dd{\bm{H}}{t} \label{1-9} \end{equation} 【拡張されたアンペールの法則】 \begin{equation} \mathrm{rot} \bm{H} = ε_{0}\dd{\bm{E}}{t} \label{1-10} \end{equation} ここで、簡単のため、電場\(\bm{E}\)と磁場\(\bm{H}\)は\(y\)と\(z\)に依存しない\(x\)だけの関数とすると、 \(\bm{E}(x,t)\)、\(\bm{H}(x,t)\)と表せるため、\eqref{1-7}、\eqref{1-8}はそれぞれ \begin{equation} \dd{E_{x}}{x} = 0 \label{1-11} \end{equation} \begin{equation} \dd{H_{x}}{x} = 0 \label{1-12} \end{equation} となり、\eqref{1-9}、\eqref{1-10}式はそれぞれ次式のようになります。 \begin{equation} \begin{pmatrix} 0\\ -\ \cfrac{\partial E_{z}}{\partial x}\\ \cfrac{\partial E_{y}}{\partial x}\\ \end{pmatrix} = \begin{pmatrix} -μ_{0}\cfrac{\partial H_{x}}{\partial t}\\ -μ_{0}\cfrac{\partial H_{y}}{\partial t}\\ -μ_{0}\cfrac{\partial H_{z}}{\partial t}\\ \end{pmatrix} \label{1-13} \end{equation} \begin{equation} \begin{pmatrix} 0\\ -\ \cfrac{\partial H_{z}}{\partial x}\\ \cfrac{\partial H_{y}}{\partial x}\\ \end{pmatrix} = \begin{pmatrix} ε_{0}\cfrac{\partial E_{x}}{\partial t}\\ ε_{0}\cfrac{\partial E_{y}}{\partial t}\\ ε_{0}\cfrac{\partial E_{z}}{\partial t}\\ \end{pmatrix} \label{1-14} \end{equation} \eqref{1-13}の両辺の第3成分を\(x\)で微分、\eqref{1-14}の両辺の第2成分を\(t\)で微分すると、それぞれ次式が得られます。 \begin{equation} \frac{\partial^2 E_{y}}{\partial x^2} = -μ_{0}\require{physics} \pdv{H_{z}}{x}{t} \label{1-15} \end{equation} \begin{equation} -\ \require{physics} \pdv{H_{z}}{t}{x} = ε_{0}\frac{\partial^2 E_{y}}{\partial t^2} \label{1-16} \end{equation} これら両式より電場\(E_{y}\)に関する次式が得られます。 \begin{equation} \frac{\partial^2 E_{y}}{\partial t^2} = \cfrac{1}{ε_{0}\ μ_{0}}\cfrac{\partial^2 E_{y}}{\partial x^2} \label{1-17} \end{equation} 同様に、\eqref{1-13}の両辺の第3成分を\(t\)で微分、\eqref{1-14}の両辺の第2成分を\(x\)で微分すると、それぞれ次式が得られます。 \begin{equation} \require{physics} \pdv{E_{y}}{t}{x} = -μ_{0}\frac{\partial^2 H_{z}}{\partial t^2} \label{1-18} \end{equation} \begin{equation} -\ \frac{\partial^2 H_{z}}{\partial x^2} = ε_{0}\require{physics} \pdv{E_{y}}{x}{t} \label{1-19} \end{equation} これら両式より磁場\(H_{z}\)に関する次式が得られます。 \begin{equation} \frac{\partial^2 H_{z}}{\partial t^2} = \cfrac{1}{ε_{0}\ μ_{0}}\cfrac{\partial^2 H_{z}}{\partial x^2} \label{1-20} \end{equation} \eqref{1-17}、\eqref{1-20}はそれぞれ電場\(\bm{E}\)と磁場\(\bm{H}\)の波動方程式であり、 その伝搬速度は光速cであり、\eqref{1-17}、\eqref{1-20}より、次式で与えられます。 \begin{equation} c = \cfrac{1}{\sqrt{ε_{0}\ μ_{0}\ }} = 3.00\ \x\ 10^8\ \mathrm{m/sec} \label{1-21} \end{equation}
(3)波動方程式の解
次式で表される\(y\)軸方向に振動し\(x\)軸の正方向に進行する電場\(E_{y}\)は、\eqref{1-17}の解となっています
(次式を\eqref{1-17}の両辺に次式を代入することにより確認できます)。
\begin{equation}
E_{y} = E_{0}\sin\ ω(\frac{x}{c}-t) \label{1-22}
\end{equation}
\eqref{1-13}の第3成分の左辺と右辺を入れ替えて\eqref{1-22}を代入すると次式が得られます。
\begin{equation}
\cfrac{\partial H_{z}}{\partial t} = -\frac{ωE_{0}}{μ_{0}c}\cos\ ω(\frac{x}{c}-t) \label{1-23}
\end{equation}
上式を時間\(t\)について積分すると次式が得られます(積分定数を0とします)。
\begin{equation}
H_{z} = H_{0}\sin\ ω(\frac{x}{c}-t) \label{1-24}
\end{equation}
ここで、
\begin{equation}
H_{0} = \frac{E_{0}}{μ_{0}c} \label{1-25}
\end{equation}
\eqref{1-24}で表わされる\(z\)軸方向に振動しx軸正方向に進行する磁場\(H_{z}\)は、\eqref{1-20}の解であることも明らかです。
以上より、電場\(E_{y}\)の波動(電波)と磁場\(H_{z}\)の波動(磁波)は
互いに直交する平面\(x-y\)面、\(x-z\)面内で同時に発生し(両者を合わせて電磁波と呼びます)、\(x\)方向に進行します(図1参照)。
このように、電磁波は、宇宙空間自体が空間的、時間的に変化する電場、磁場(電磁波)を発生し、伝搬する性質を有しており、
発生した電磁波が空間中を光速cで伝搬します。
これにより、電磁波の伝搬のために「エーテル」のような媒体の存在は必要ではないことがわかりました。
なお、電磁波により運ばれるエネルギー密度は次式のポインティングベクトル\(\bm{S}\)で表されます。
\begin{equation}
\bm{S} = \bm{E} \x \bm{H} \label{1-26}
\end{equation}
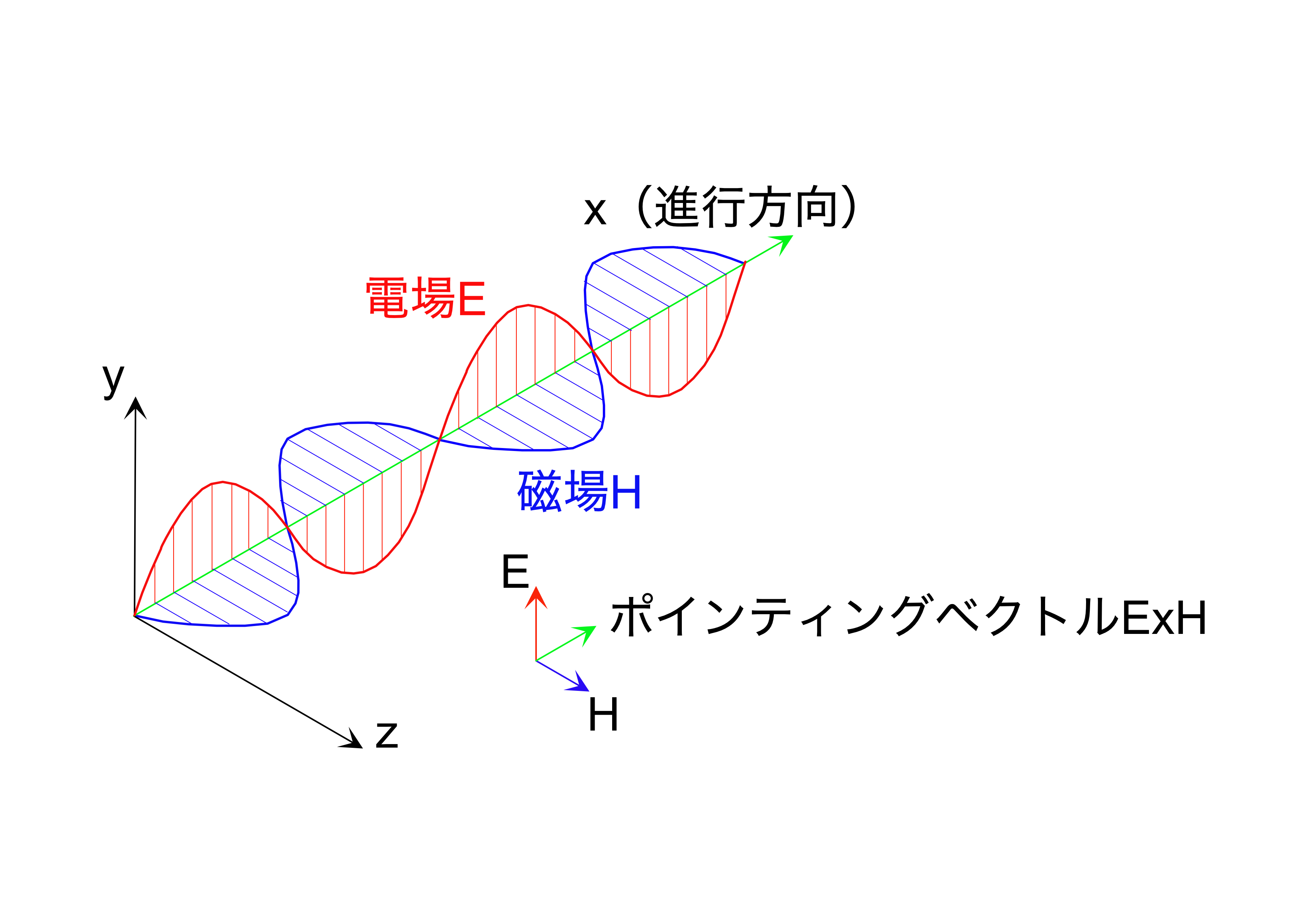
図1 電磁波
以上より、現象論的には下記のことが言えます。
ファラデーの法則\eqref{1-9}と拡張されたアンペールの法則\eqref{1-10}より、磁場の変化と電場の変化とは相互に関係しており、
磁場が変化するとそれに応じて電場が変化し、磁場が変化するとそれに応じて電場が変化することとなります。
したがって、真空空間において磁場(または電場)が変化すると、電場(または磁場)の変化により磁場の波動(「磁波」と呼びます)(波動方程式\eqref{1-20})
(または電場の波動(「電波」と呼びます)(波動方程式\eqref{1-17}))が発生し、
その発生した磁波(または電波)に対応して同時に電波(波動方程式\eqref{1-17})(または磁波(波動方程式\eqref{1-20}))が発生します。
そして、磁場(または電場)の変化に対する発生する電場(または磁場)の方向は、ファラデーの法則\eqref{1-9}(またはアンペールの法則\eqref{1-10})より直交する方向となるため、
磁波と電波の発生する方向は図1に示されるように直交します。
【コラム5】光速\( c \)が慣性系によらず不変である理由
電電場と磁場の相互作用として、電場の発生・変化により磁場が発生・変化し、又はその逆に磁場の発生・変化による電場が発生・変化し、
その電磁場の発生・変化が電磁波として遠方に光速\( c \)で進行していくものです。
ここで、本文において(20)式及び(21)式によりそれぞれ表される電磁波の方程式及び光速は、慣性系をと特定せずに任意の慣性系において成立するものです。
したがって、任意の慣性系に対して光速は不変となります。
例えば、下記(1)項及び(2)項により発生する電磁波の光速について考えてみます。
(1) 電荷の運動による電磁波の発生
電荷を有する荷電粒子(電荷)\(q\)の運動、すなわち電流\( I=dq/dt \)の発生があると、電流の微小長さ(線素)\( d\bm{l} \)によって距離\( \bm{r} \)の点には
ビオ・サバールの法則(アンペールの法則から誘導できます)
\begin{equation}
d\bm{H} = \cfrac{I}{4\pi} \cfrac{d\bm{l} \x \bm{r}}{r^{3}} \label{c5-1}
\end{equation}
により、磁界\( d\bm{H} \)が発生します。
その結果、本文中に説明したように、新たな磁場の発生より電場が発生し、順次、電場と磁場の発生が繰り返されることにより、
電磁波が光速\( c \)で進行していくことになります。
上記において、電荷\( q \)が速度\( v \)で流れる(例えば室内)空間を慣性系A、電荷に固定した慣性系を慣性系Bとすると、
慣性系Aにおいて観測される光速\( c_{A} \)のみならず、慣性系Aに対して速度\( v \)で運動する慣性系Bにおいて観測される光速\( c_{B} \)も電磁波方程式から導出された光速\( c \)となります。
\begin{equation}
c_{A} = c_{B} =c \label{c5-2}
\end{equation}
慣性系Bにおいても、慣性系Aと同一の電磁波方程式及び光速が適用されるからです。
(2) 電磁誘導による電磁波の発生
磁束密度\( \bm{B} \)がある場において磁束を切るように導体を速度\( \bm{v} \)で運動させると、電磁誘導の法則(本文(9)式)により、導体内に
\begin{equation}
\bm{E} = \bm{v} \x \bm{B} \label{c5-3}
\end{equation}
の電場が発生します。
その結果、この電場の発生により周囲の磁界が変化し、それにより電場も変化し、順次、電場の変化と磁場の変化が繰り返されることにより、
電磁波が光速\( c \)で進行していくことになります。
上記において、磁束密度\( \bm{B} \)を発生させている(例えば室内)空間を慣性系A、速度\( \bm{v} \)で運動する導体に固定した空間を慣性系Bとすると。(1)項と同様に、
慣性系Aにおいて観測される光速\( c_{A} \)のみならず、慣性系Aに対して速度\( v \)で運動する慣性系Bにおいて観測される光速\( c_{B} \)も電磁波方程式から導出された光速\( c \)となります。
\begin{equation}
c_{A} = c_{B} =c \label{c5-4}
\end{equation}
慣性系Bにおいても、慣性系Aと同一の電磁波方程式及び光速が適用されるからです。