Ⅶ ミンコフスキー時空
従来のニュートン力学の基礎となるガリレーの相対性原理のもとでは、空間(座標)と時間とが関連付けられておらず、
時間は空間座標とは独立して進行する絶対時間であるのに対して、特殊相対性理論のものでは、時間は空間に対して独立ではなく、空間と時間が相互に関連しています。
この特殊相対性理論に基づく現象は、我々の通常経験するものとは異なりますが、時間と空間が一体化したものであり、その結果として、
高速運動する物体の長さが収縮(ローレンツ収縮)したり、時間の経過が遅くなりします。
そこで、相対性理論においては、空間座標(\(x, y, z\))に時間座標ctを加えた4次元座標(\(ct, x, y, z\))として取り扱うこととしています。
このような4次元座標による空間をミンコフスキー時空またはミンコフスキー空間といいます。
このミンコフスキー時空を視覚的に理解できるように便宜上空間座標を2次元(\(x、y\))、
すなわち時空3次元(\(ct、x、y\))として表現したものが図1となります。
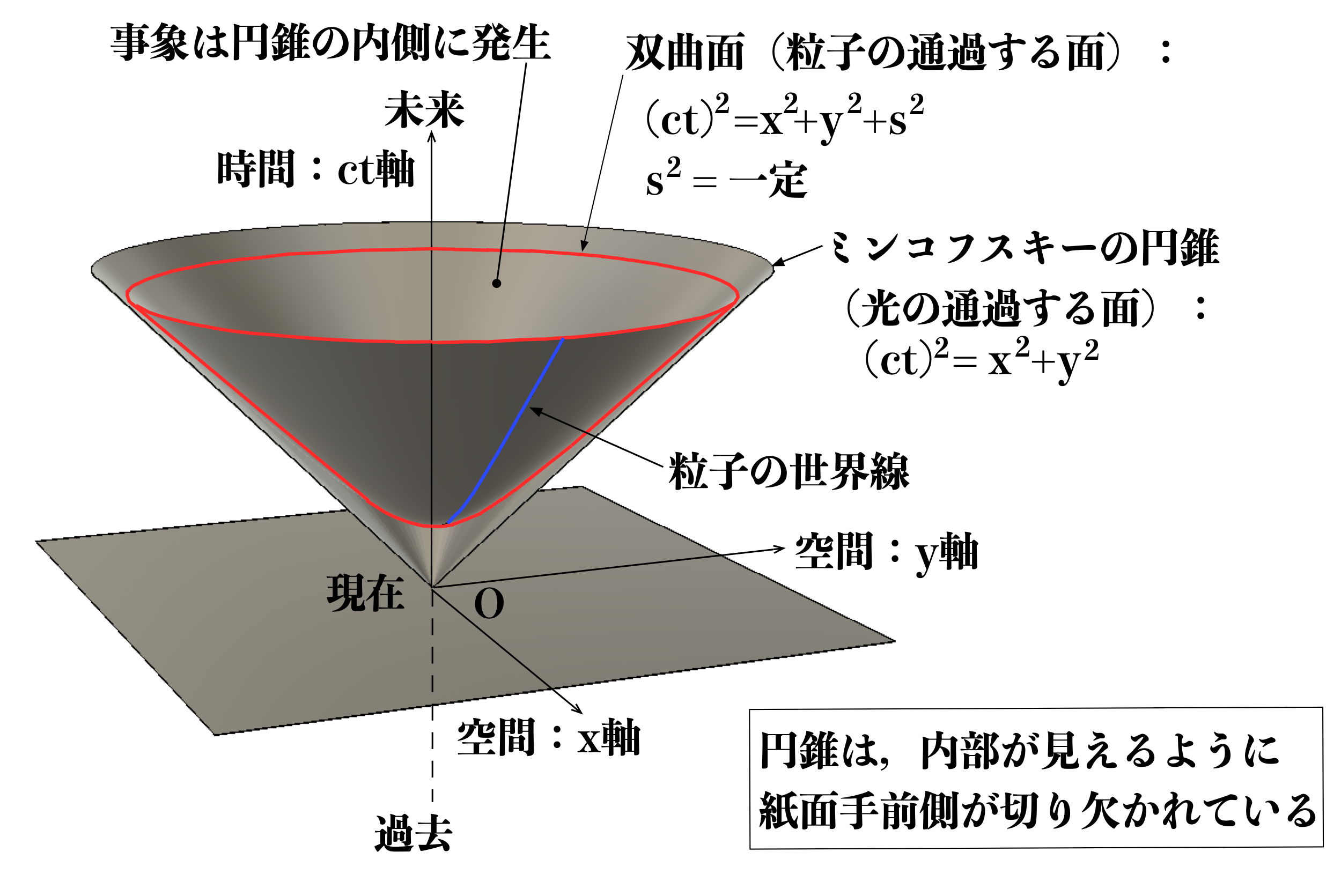
図1 3次元(\(ct, x, y\))のミンコフスキー時空
相対性理論において対象となる出来事を事象といい、事象はミンコフスキー時空においては1つの点として表現し、ミンコフスキー時空における1点は世界点と呼ばれます。
質点の運動はミンコフスキー時空では一般に曲線として表現され、それを世界線と呼びます。
2つの世界点(\(ct_{1},x_{1},y_{1},z_{1}\))と(\(ct_{2},x_{2},y_{2},z_{2}\))の間の量\({s_{12}}^{2}\)を
\begin{equation}
{s_{12}}^{2} = -(ct_{2}-ct_{1})^{2} + (x_{2}-x_{1})^{2} + (y_{2}-y_{1})^{2} + (z_{2}-z_{1})^{2} \label{3-1}
\end{equation}
で定義したとき、\(s_{12}\)を世界間隔と呼びます。
世界間隔は空間座標の3次元空間における距離をミンコフスキー時空に拡大したものです。
したがって、ミンコフスキー時空の2つの世界点(\(ct,x,y,z\))と(\(ct+d(ct),\ x+dx,\ y+dy,\ z+dz\))の間の世界間隔は次式により求まる\(ds\)となります。
\begin{equation}
ds^{2} = -(cdt)^{2} + dx^{2} + dy^{2} + dz^{2} \label{3-2}
\end{equation}
K座標系の点P(\(ct, x, y, z\))を座標変換したK'座標系のP'(\(ct', x', y', z'\))について下記式により定義された\(s^{2}\)、\(s’^{2}\) は、
ローレンツ変換の式を用いると
\begin{equation}
s^{2}=-(c\ t)^{2}+x^{2}+y^{2}+z^{2}= -(c\ t'\ )^{2}+x'\ ^{2}+y'\ ^{2}+z'\ ^{2}=s'\ ^{2} = \mathrm{Const(一定)} \label{3-3}
\end{equation}
となり、異なる観測系(時空)において\(s^{2}\)が一定となります。
\(s, s'\)は、3次元空間におけるそれぞれの座標の原点から点P、P'までの距離の相当するものであり、「世界長さ」と呼ばれています。
ミンコフスキー時空の空間座標を2次元の平面(\(xーy\)座標)に垂直な方向を時間軸(\(ct\)軸)とする3次元座標系(\(ct, x, y\))で考えると、
\begin{equation}
-(c\ t)^{2}+x^{2}+y^{2} = \mathrm{Const(一定)} \label{3-4}
\end{equation}
の表す曲面は双曲面(二葉回転双曲面)となります(図1参照)。
ミンコフスキー時空では、原点を通過する光は次式で表される円錐(原点を通り時間軸から45度傾いた円錐であり、ミンコフスキー円錐といいます。)の上を通過することになります。
そこで、ミンコフスキー円錐を光円錐ともいいます。
\begin{equation}
-(c\ t)^{2}+x^{2}+y^{2}+z^{2} = 0 \label{3-5}
\end{equation}
ミンコフスキー時空で発生する事象の範囲は\eqref{3-4}を満たす座標(\(ct, x, y, z\))の集合となるため、ミンコフスキー円錐の内側となります(図1参照)。