Ⅷ 時空図
ミンコフスキー時空は、正確には4次元(時間座標が1次元、空間座標が3次元)ですが、静止座標系Kと移動座標系K’を取り扱う場合は、
移動座標系K'の運動方向を静止座標系Kの\(x\)方向として処理することにより、空間座標については静止座標Kの\(x\)座標のみとして処理することが可能です。
したがって、通常、ミンコフスキー時空を図1のような2次元(\(ct, x\))として表現、検討することができるため(文献(1))、
有用です。
そこで、時空図について簡単に説明します。
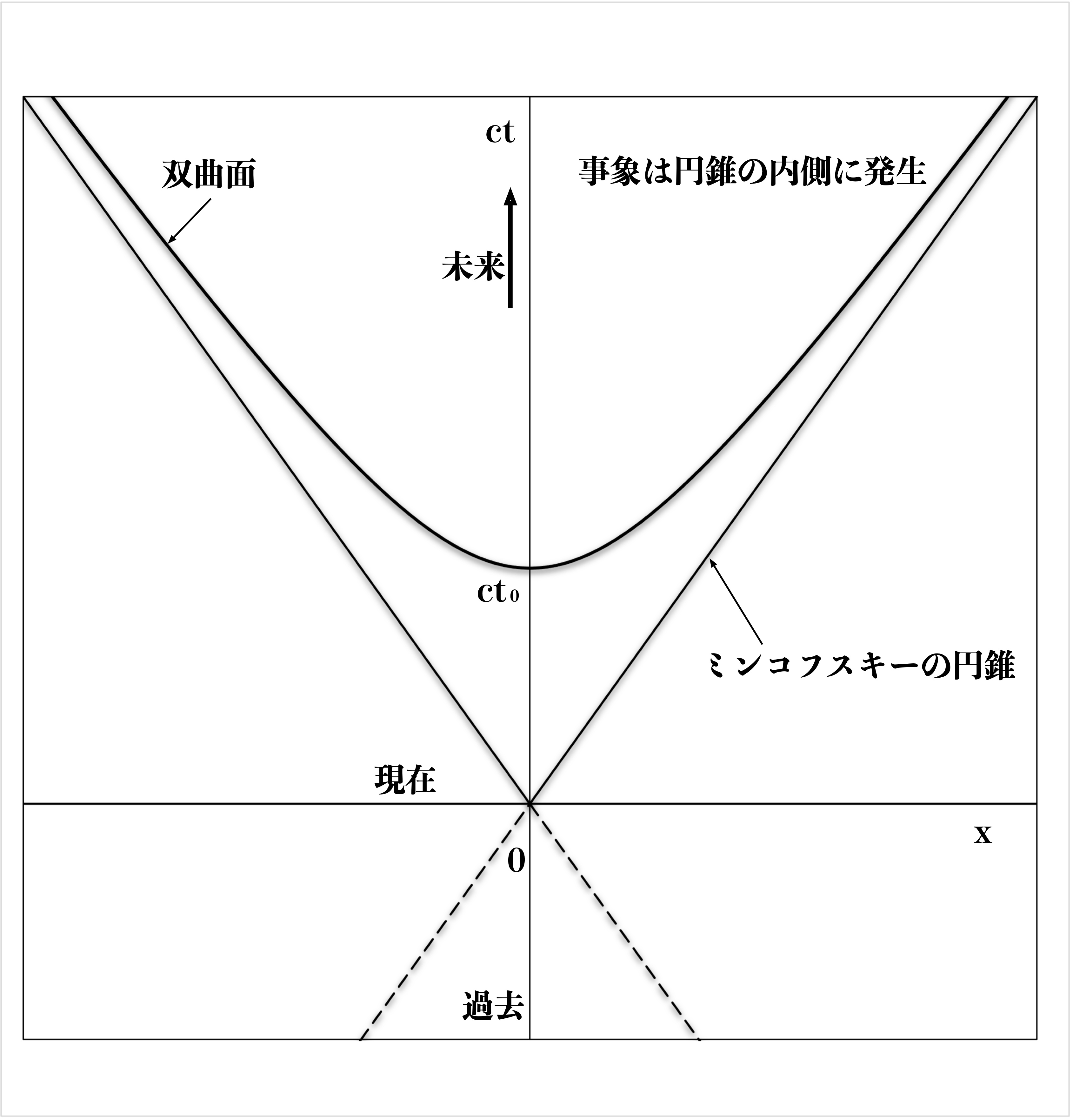
図1 時空図
1.基本時空図
慣性系K(\(ct, x\))に対して\(x\)軸方向に速度\(v\)で相対運動する慣性系K'(\(ct', x'\))について、
慣性系Kを静止しているとした時空図は図2のように表されます。
静止している慣性系Kでは時間(座標)\(ct\)が \(x=0\) の状態で鉛直上方に向かって直線的に増加するのに対して、
運動している慣性系K'では時間(座標)\(ct'\)は傾き\(c/v\)(\(=1/β\))の直線、および空間座標\(x'\)は傾き\(v/c\)(=β)の直線に乗って増加します。
光は傾き1の直線により増加し、慣性系K'の相対速度\(v\)が増加すると\(ct'\)の直線の傾きが小さくなるとともに\(x'\)の傾きが大きくなり、
光の傾きに近づいていきます。
なお、慣性系K'は慣性系Kをローレンツ変換したものですが、幾何学的には慣性系K'の座標軸は
(構成する座標軸が直交しない)斜交座標となります。
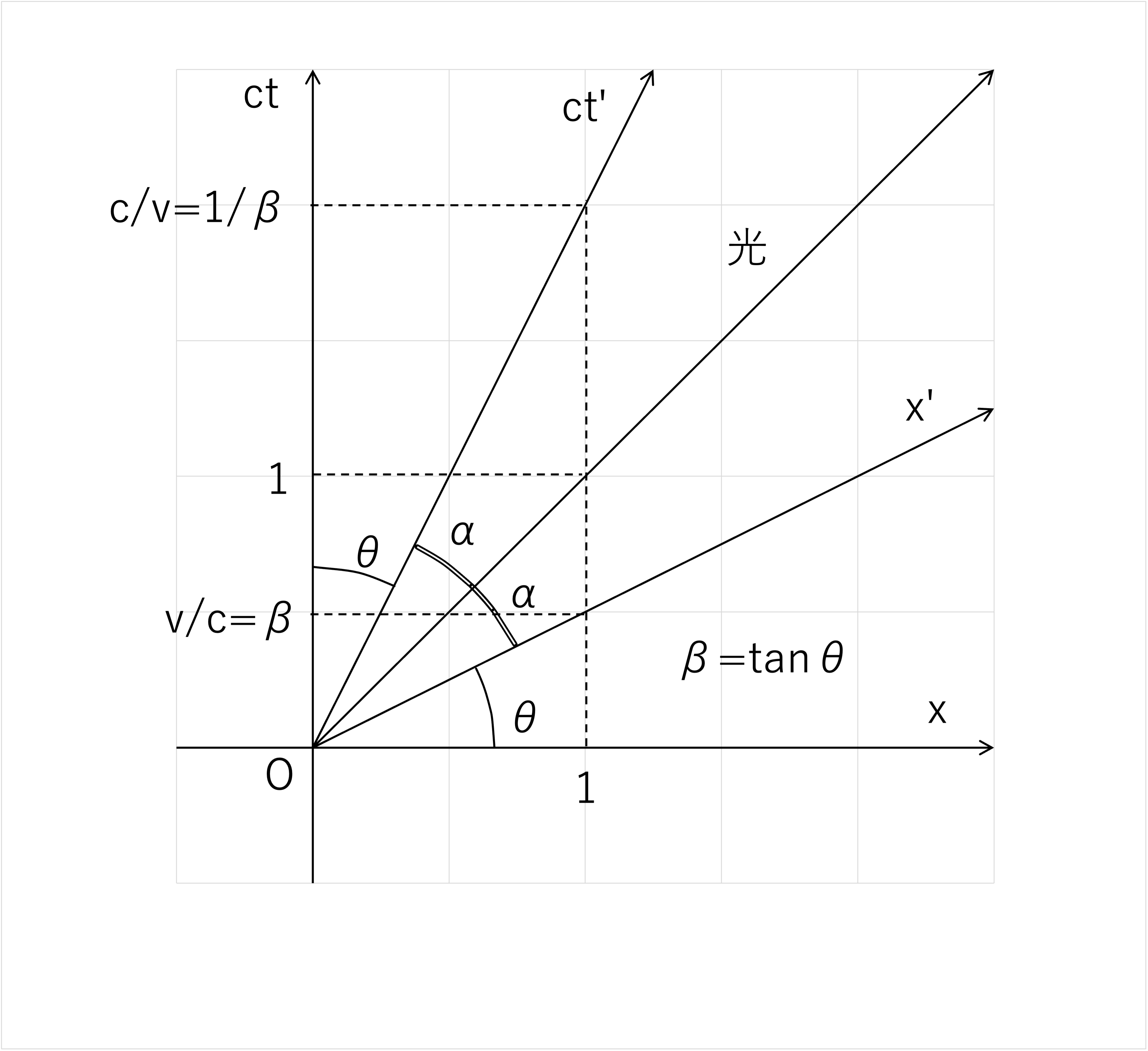
図2 基本時空図
2.運動物体内の時間の遅れの時空図
運動物体内の時間の遅れを時空図で表示することについて説明します。
静止する座標系K(\(ct, x\))に対して速度\(v=βc\)(\(0\leqq β\lt 1\))で運動するを座標系K'(\(ct', x'\))について、
それぞれの座標系から観測した場合の相手の座標系の時間を遅れを表示する時空図が図3です。
図3では、出発時の2つの座標系の時刻を\(ct=ct'=0\)(光年)に合わせて座標系K'を座標系Kの\(x\)軸方向に速度\(v\)で運動を開始し、
座標系K'が距離\(b\)(光年)に到達した時点でそれぞれの座標系から相手の座標系固定の経過時間(時刻)を観測します。
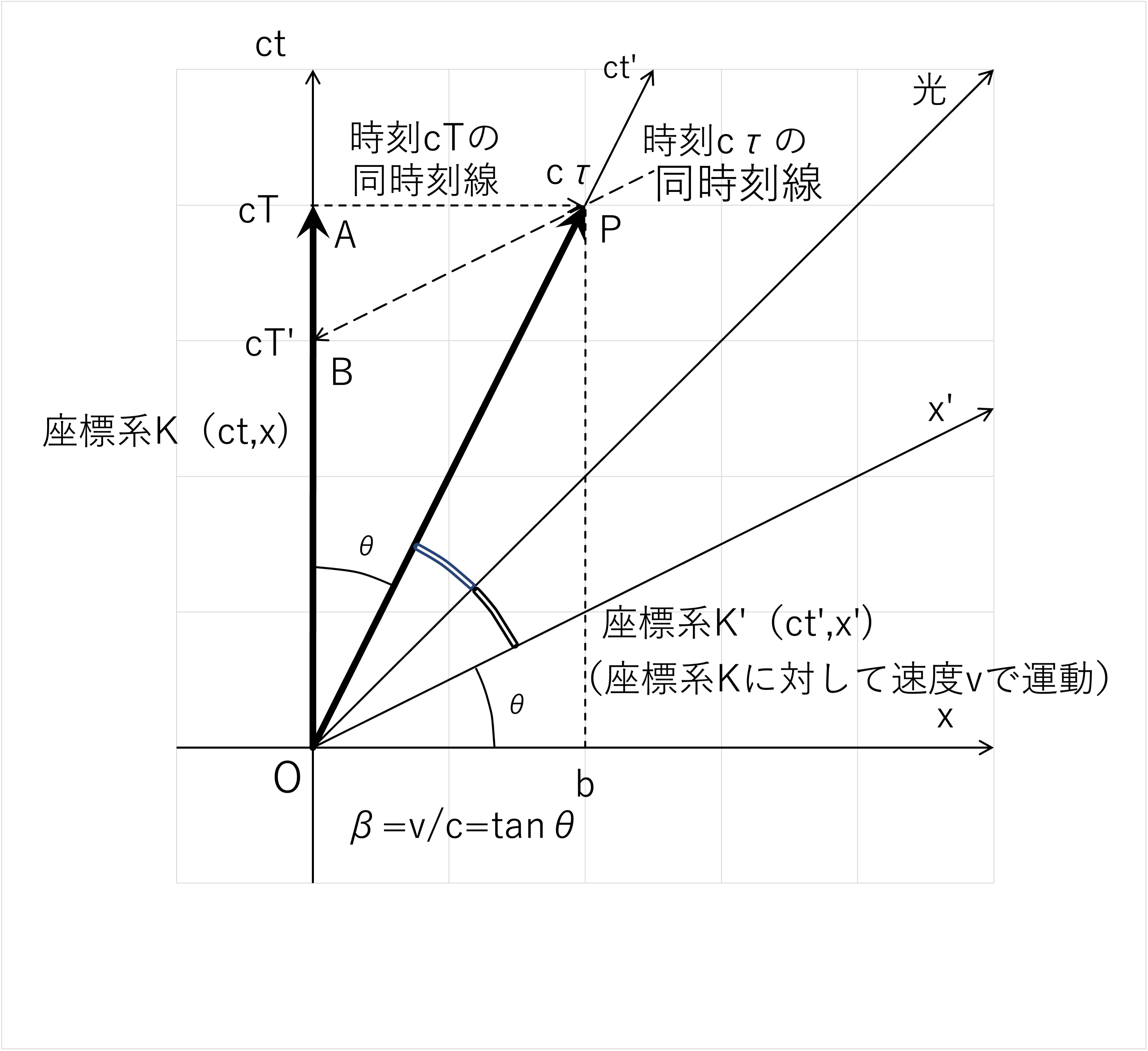
図3 運動物体内の時間の遅れの時空図
(1) 座標系Kから観測した座標系K'固定時計の時間遅れ
座標系Kにおける世界点Aの同時刻は世界点Aを通りx軸に平行な直線上の世界点(の集合)となります。このため、座標系Kから座標系K'を観測したときに
(座標系Kの)世界点Aと同時刻にある(座標系K'の)世界点はPとなります。
したがって、座標系Kから座標系K'を観測したときの座標系K'固定時計の時刻は\(cτ\)であり、
τは「Ⅲ 基本原理から導かれる現象等」ページの(6)式において
\(T\)をτに置換した次式により求まります。
\(τ=t\sqrt{1-β^{2}}\)
なお、「Ⅴ 座標変換」ページの(3)より、0\(\lt\sqrt{1-β^{2}}\leqq1\)
(2) 座標系K'から観測した座標系K固定時計の時間遅れ
上記と逆に座標系K'が静止し、座標系Kが運動している場合となります。
座標系K'における世界点Pの同時刻は世界点Pを通り\(x'\)軸に平行な直線上の世界点(の集合)となります。
このため、座標系K'から座標系Kを観測したときに(座標系K'の)世界点Pと同時刻にある(座標系Kの)世界点はBとなります。
したがって、座標系K'から座標系Kを観測したときの座標系K固定時計の時刻は\(cT'\)となります。
ここで、「Ⅲ 基本原理から導かれる現象等」ページの(6)式において\(T\)は静止座標系固定時計の時間、\(t\)は運動座標系固定時計の時間であるため、
\(T'\)は、同(6)式において
\(T\)、\(t\)をそれぞれ\(T'\)、τに置き換えた下記式に求まります。
\(T'=τ\sqrt{1-β^{2}}\)
3.Ⅲ章4項「例題3」の時空図
列車座標系K'(\(ct', x'\))を基準(静止)座標系、地面座標系K(\(ct, x\))を相対運動系として描いた時空図が図4です。
各座標系の時間座標軸\(ct\)又は\(ct'\)の各時刻に対して空間座標軸\(x'\)又は\(x\)に平行な直線上にある事象がそれぞれの座標系の同時刻に発生したものとなります。
なお、この時空図は列車座標系K'を基準座標系として描いており、地面座標系Kは列車座標系K'に対して速度\(-v\)で運動しているため、
列車座標軸K'の時間座標軸\(ct'\)、空間座標軸\(x'\)に対する地面座標系Kの時間座標軸\(ct\)、
空間座標軸\(x\)の直線の傾きの方向が前記「基本的時空図」とは逆になっています。
列車座標系K'では先端Aと後端Bに対応する事象Fと事象Rは時間座標軸\(ct'\)の時刻\(ct'0\)に発生していることがわかります。
これに対して、地面座標系Kでは後端Bに対応する事象Rは時間軸\(ct\)の\(ct1\)に発生し、
先端Aに対応する事象Fは時間軸\(ct\)の\(ct2\)に発生しており、時間的には\(ct1\)が\(ct2\)より前になります。
したがって、地面座標系Kにおいて、ビーム光は先端より後端の方に先に到着しており、同時ではないことが観測されることがわかります。
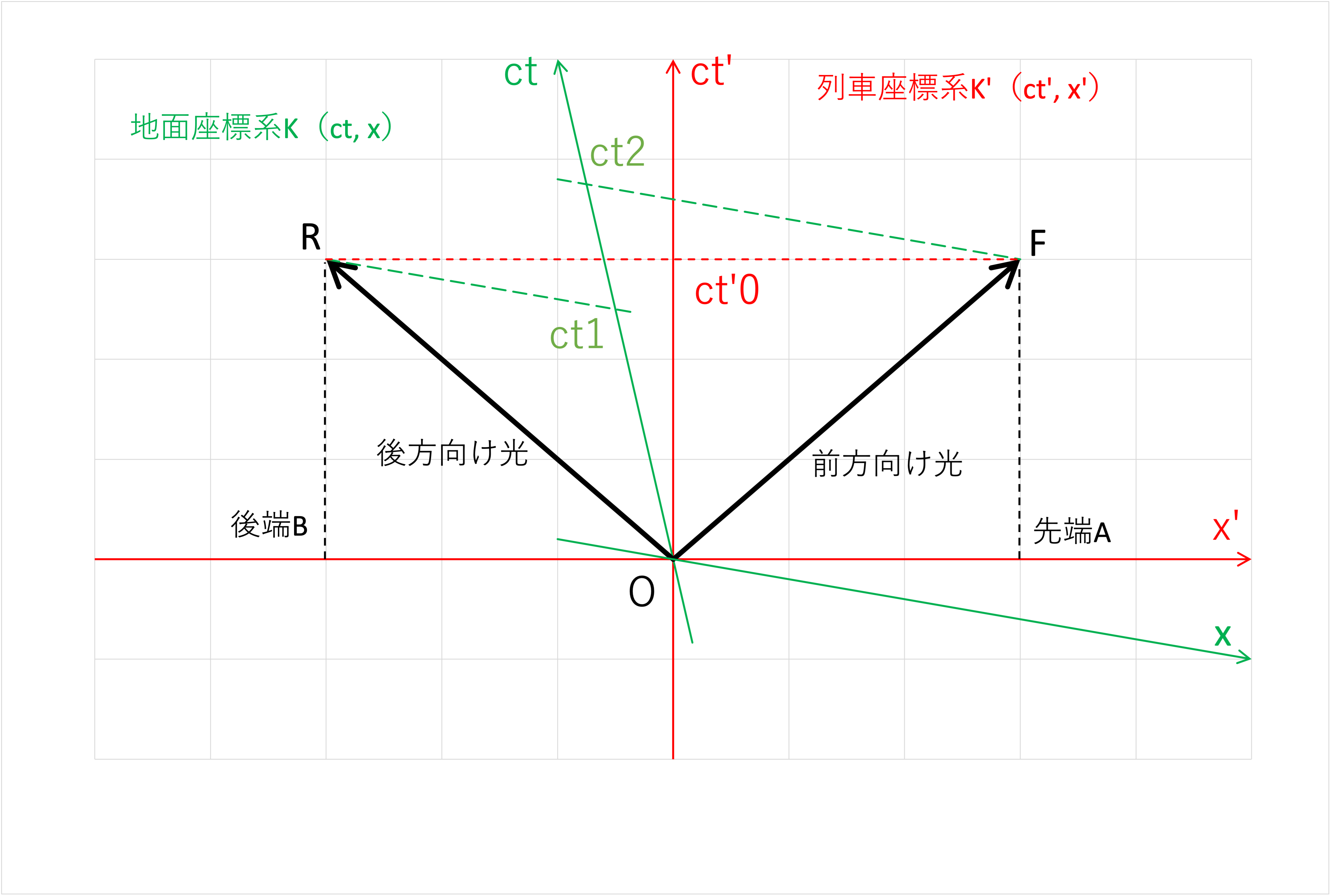
図4 \(Ⅲ\)章4項「例題3」の時空図
【文献】
(1) 見城尚志、佐野茂:”幾何で見える必ずわかる一般相対性理論”、pp.216-217、初版、2022年10月7日、株式会社技術評論社。