7 数学的準備
特殊相対性理論と異なり、一般相対性理論は高度な数学的知識等により組み立てられているため、
より深く理解するためにそれらの数学的知識等の概要を紹介します。
7.1 空間座標系
3次元空間を例にとれば、代表的な空間座標系は、直交座標系(デカルト座標系)、斜交座標系、
曲線座標系があります(図1参照)。
これらの座標系の座標軸に沿った各ベクトルは基底ベクトルと呼ばれ、大きさと方向を持ち、
その空間内の任意のベクトルの大きさと方向を表示することができます(図1の\(\bm{e} _{1},\bm{e} _{2},\bm{e} _{3}\))。
基底ベクトルの大きさと方向は、直線座標系と斜交座標系においては空間の位置に関係なく一定ですが、
曲線座標系においては座標軸の位置により変化しています。
すなわち、曲線座標系の基底ベクトルの位置と方向は空間位置の関数となっています。
ただし、局所的には、曲線座標系は直線座標系、特に斜交座標系で近似することができ、
一般相対性理論では、曲線座標系で取り扱われます。
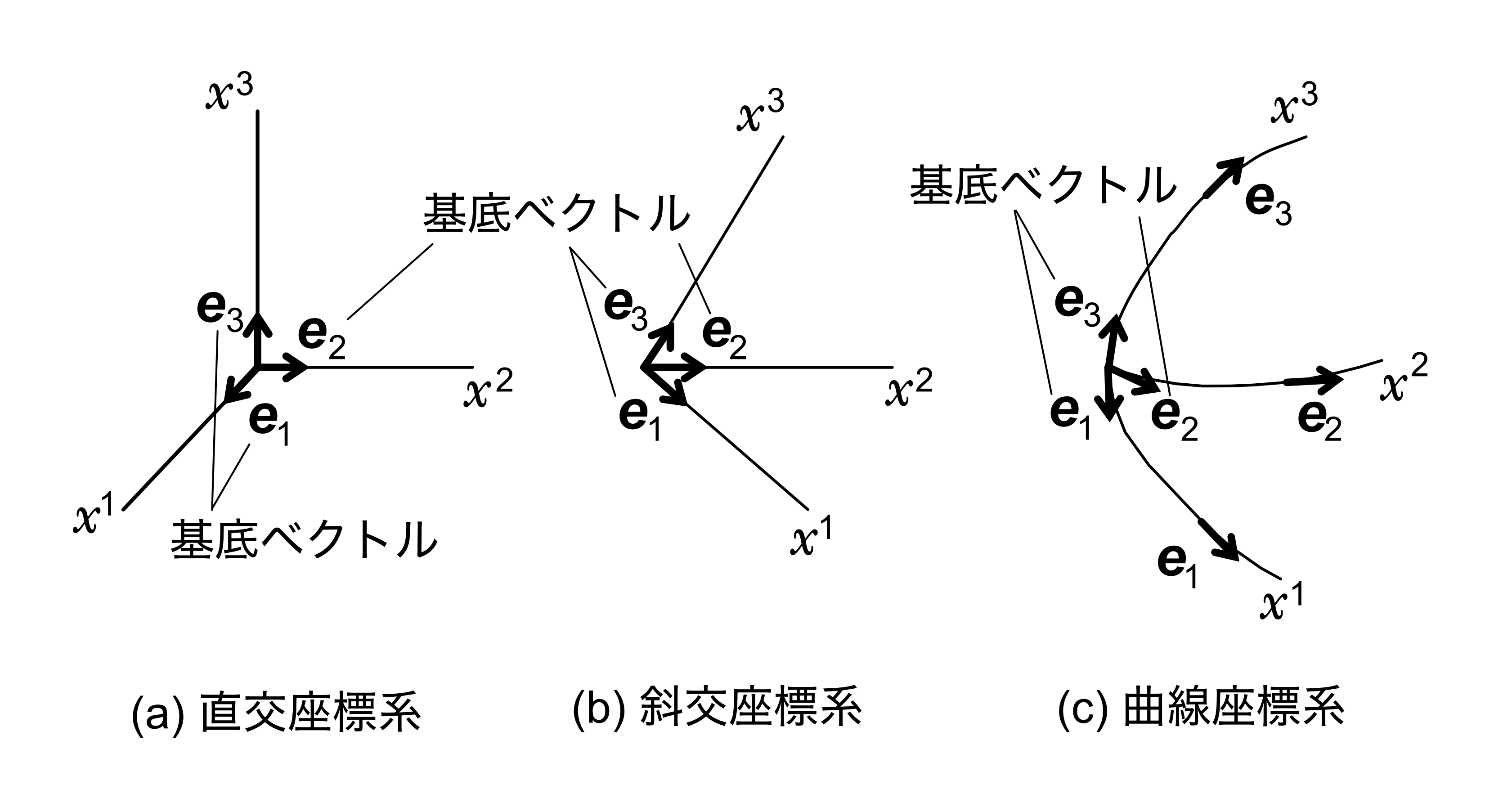
図1 3次元空間座標系
7.2 ベクトル
直交座標系および斜交座標系においては、図1(a)、(b)に示されるように、任意のベクトル\(\bm A\)はその座標軸成分(\(A^{1},A^{2},A^{3}\)) と基底ベクトル(\(\bm e _{1},\bm e _{2},\bm e _{3}\) )の一次結合により次式のようなベクトル和で表されます (2次元空間における各座標系のベクトル表示を図1に示します)。 なお、\eqref{a2-1}最右辺はアインシュタインの省略(項中に共通する添字があるときに和記号\(\sum\)を省略)で表したものです。 \begin{equation} \bm A = A^{1}\bm e_{1} + A^{2}\bm e_{2} + A^{3}\bm e_{3} = \sum_{\mu = 1}^{3}A^{\mu} \bm e_{\mu} \equiv A^{\mu}e_{\mu} \label{a2-1} \end{equation} 局所座標系では基底ベクトルはその大きさと方向が座標の位置により変化するが、 局所的には斜交座標系とみなして任意のベクトル\(\bm A\)は各座標軸の基底ベクトルを基準としたベクトルの和として \eqref{a2-1}のように表すことができます。

図1 2次元空間における各座標系のベクトル
以上のように、曲線座標系においては局所的に斜交座標系とみなすので、
斜交座標系について少し補足説明しておきます。
斜交座標系における座標軸成分\(A^{\mu}\)(\(\mu =1,2,3\)。以下同様)は、図3(a)に示すように
座標軸\(x^{\mu}\)にそれぞれ平行な成分であり、ベクトル\(\bm A\)の反変成分といい、
反変成分を表すために添字は成分の右肩に付けます。
これに対して、斜交座標系においてベクトル\(\bm A\)を図3(b)に示すように各座標軸\(x^{\mu}\)に垂直に下した成分
\(A_{\mu}\)により表すこともできます。
このように表した座標軸成分 \(A_{\mu}\)をベクトルの共変成分といい、
共変成分を表すために添字は成分の右下に付けます。
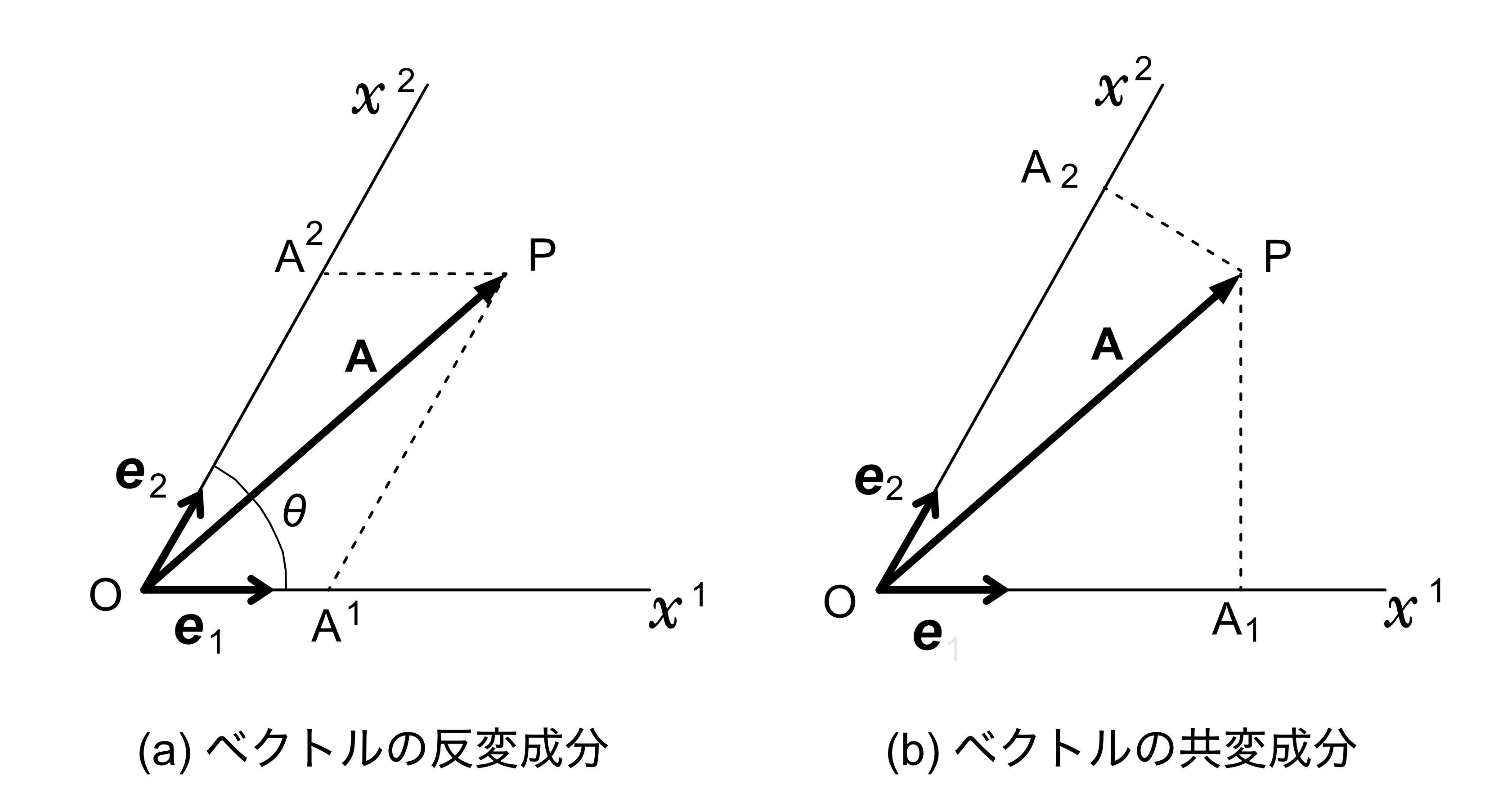
図3 2次元空間におけるベクトルの反変成分と共変成分
反変成分\(A_{\mu}\)はそれぞれ\(\bm e_{\mu}\)方向への正射影であるため、次式が得られます。
\begin{equation}
A_{\mu} = \bm A \cdot \bm e_{\mu} \label{a2-2}
\end{equation}
ここで、右辺の「\(\cdot\)」は内積を表す演算記号です。
\eqref{a2-2}に\eqref{a2-1}を代入すると、次式が得られます。
\begin{equation}
A_{\mu} = (\sum_{\nu=1}^{3}A^{\nu}\bm e_{\nu})\cdot \bm e_{\mu} = \sum_{\nu=1}^{3}A^{\nu}(\bm e_{\nu} \cdot \bm e_{\mu})
= \sum_{\nu=1}^{3} g_{\mu \nu}A^{\nu} \label{a2-3}
\end{equation}
ここで、\(g_{\mu\nu}\)は基底ベクトル\(\bm e_{\mu}\)と\(\bm e_{\nu}\)の内積であり、次式で表されます(図3(a)参照)。
\begin{equation}
g_{\mu\nu} = g_{\nu\mu} = \bm e_{\mu} \cdot \bm e_{\nu} = | \bm e _{\mu}| | \bm e _{\nu}| \cos θ_{\mu\nu} \label{a2-4}
\end{equation}
行列[\(g_{\mu\nu}\)]を行列表記すると
\begin{align}
[g_{\mu\nu}] = [\bm e _{\mu} \cdot \bm e_{\nu}] &=
\begin{pmatrix}
\bm e_{1} \\
\bm e_{2} \\
\bm e_{3}
\end{pmatrix}
\cdot \Bigl( \bm e_{1} \quad \bm e_{2} \quad \bm e_{3} \Bigr) \notag \\
&=
\begin{pmatrix}
\bm e_{1}\cdot \bm e_{1} & \bm e_{1}\cdot \bm e_{2} & \bm e_{1}\cdot \bm e_{3} \\
\bm e_{2}\cdot \bm e_{1} & \bm e_{2}\cdot \bm e_{2} & \bm e_{2}\cdot \bm e_{3} \\
\bm e_{3}\cdot \bm e_{1} & \bm e_{3}\cdot \bm e_{2} & \bm e_{3}\cdot \bm e_{3}
\end{pmatrix} \notag \\
&=
\begin{pmatrix}
g_{11} & g_{12} & g_{13} \\
g_{21} & g_{22} & g_{23} \\
g_{31} & g_{32} & g_{33}
\end{pmatrix} \label{a2-5}
\end{align}
となるため、\eqref{a2-3}を行列表記すると次式が得られます。
\begin{align}
\begin{pmatrix}
A_{1} \\
A_{2} \\
A_{3}
\end{pmatrix}
&=
\begin{pmatrix}
g_{11} & g_{12} & g_{13} \\
g_{21} & g_{22} & g_{23} \\
g_{31} & g_{32} & g_{33}
\end{pmatrix}
\begin{pmatrix}
A^{1} \\
A^{2} \\
A^{3}
\end{pmatrix} \label{a2-6}
\end{align}
\(g_{\mu\mu}\)は同一基底ベクトルどうしの内積であるため、次式が成立します。
なお、\eqref{a2-3}、\eqref{a2-6}より、\(g_{\mu\nu}\)はテンソル(次項3.テンソル参照)となります。
\begin{equation}
g_{\mu\mu} = \bm e_{\mu} \cdot \bm e_{\mu} = {e_{\mu}}^{2} \label{a2-7}
\end{equation}
行列\(g_{\mu\nu}\)の逆行列を\(g^{\mu\nu}\)で表すこととすると、次式が成立します。
\begin{equation}
g_{\mu\nu}g^{\mu\nu} = {δ^{\mu}}_{\nu} \label{a2-8}
\end{equation}
ここで、\({δ^{\mu}}_{\nu}\)はクロネッカーのデルタであり、次式で表されます。
\begin{equation}
{δ^{\mu}}_{\nu} =
\begin{pmatrix}
1\ & 0\ & 0\ \\
0\ & 1\ & 0\ \\
0\ & 0\ & 1\
\end{pmatrix}
\label{a2-9}
\end{equation}
7.3 テンソル
アインシュタインの重力方程式はテンソル方程式として表現されます。
そこで、テンソルの概要を説明します。
テンソルとは、ベクトルを別のベクトルに変換する線形作用素をいいます。
ベクトル\(\bm p\)(\(p^{1}\ p^{2}\ p^{3}\))、\(\bm q\)(\(q_{1}\ q_{2}\ q_{3}\))、
テンソル\(T\)として、ベクトル\(\bm p\)をベクトル\(\bm q\)への変換を数式および行列形式で表すとそれぞれ\eqref{a3-1}および\eqref{a3-2}となります。
\begin{equation}
q_{\mu} = \sum_{\nu=1}^{3}T_{\mu\nu}p^{\nu} = T_{\mu\nu}p^{\nu} \label{a3-1}
\end{equation}
\begin{align}
\begin{pmatrix}
q_{1} \\
q_{2} \\
q_{3}
\end{pmatrix}
&=
\begin{pmatrix}
T_{11} & T_{12} & T_{13} \\
T_{21} & T_{22} & T_{23} \\
T_{31} & T_{32} & T_{33}
\end{pmatrix}
\begin{pmatrix}
p^{1} \\
p^{2} \\
p^{3}
\end{pmatrix} \label{a3-2}
\end{align}
テンソルは線形作用素であるため、スカラーα、β、ベクトル\(\bm p,\ \bm q\)について次式が成立します。
\begin{equation}
T(α\bm p + β\bm q) = αT(\bm p) + βT(\bm q) \label{a3-3}
\end{equation}