6 シュバルツシルト時空
質量の分布が球対称で時間的変化のない時空は最も基本的な時空であり、シュバルツシルト時空と呼ばれ、 水星の近日点移動や強い重力場の光の湾曲等の検証についても利用されています。
6.1 シュバルツシルト解
(1)シュバルツシルト解
質量の分布が球対称で時間的変化のない重力場(時空)の計量を求めたのがシュバルツシルト解です。
例えば、太陽の近傍に存在する小さな惑星(水星)の運動の求めるために利用されます。
座標系は図1に示す球座標系
\[
x^{0}=ct,\ x^{1}=r,\ x^{2}=θ,\ x^{3}=\phi
\]
を使用し、原点Oに質量\(M\)の質点があり、周囲は真空とします。
一般的には、計量テンソルの自由度は10ですが、球対称、時間不変という対称性から自由度は減少します。
これによりテンソルの形は限られたものとなります。
原点Oに質量Mの質点があり、その周囲は真空であるため、原点以外はエネルギー運動量テンソル\(T_{ij}\)は0となるため、
次式で表される計量テンソル\(g_{ij}\)が得られます。
\begin{equation}
g_{ij}=
\begin{pmatrix}
g_{00} & 0 & 0 & 0 \\
0 & g_{11} & 0 & 0 \\
0 & 0 & g_{22} & 0 \\
0 & 0 & 0 & g_{33}
\end{pmatrix}
=
\begin{pmatrix}
-1+\cfrac{R_{s}}{r} & 0 & 0 & 0 \\
0 & \Bigl(1-\cfrac{R_{s}}{r}\Bigr)^{-1} & 0 & 0 \\
0 & 0 & r^{2} & 0 \\
0 & 0 & 0 & r^{2}\sin^{2}θ
\end{pmatrix} \label{f1-1}
\end{equation}
ここで、
\begin{equation}
R_{s} = \cfrac{2GM}{c^{2}} \label{f1-2}
\end{equation}
であり、シュバルツシルト半径または重力半径と呼びます。
これより計量\(ds^{2}\)は次式のとおりとなります。
\begin{equation}
ds^{2} = -\Bigl(1-\cfrac{R_{s}}{r}\Bigr)(cdt)^{2} + \cfrac{1}{1-\cfrac{R_{s}}{r}}dr^{2} + r^{2}(dθ^{2}+\sin^{2}θd\phi^{2}) \label{f1-3}
\end{equation}
重力場方程式のこの解を「シュバルツシルト解」、この計量を「シュバルツシルト計量」と呼びます。
質点から十分遠方(\(r \gg R_{s}\))では計量は
\begin{equation}
ds^{2} = -(cdt)^{2} + dr^{2} + r^{2}(dθ^{2}+\sin^{2}θd\phi^{2}) \label{f1-4}
\end{equation}
となり、ニュートンの万有引力の法則と一致します。
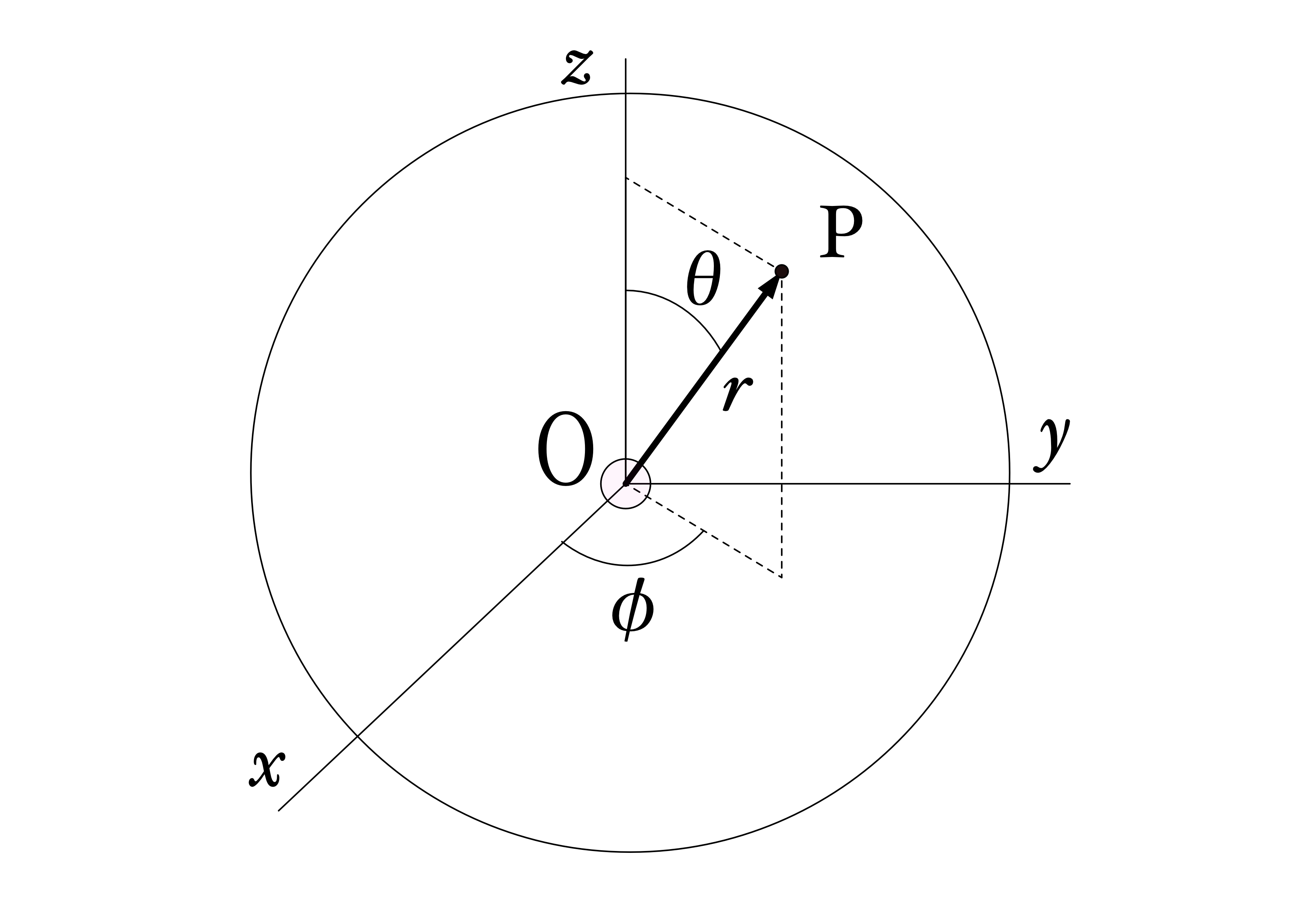
図1 球座標系
(2)シュバルツシルト半径の意義
質量\(M\)の物体Aから無限遠方\(r = \infty \)にある静止している質量\(m\)の物体Bが物体Aの引力により加速しつつ落下するときの速度を\(v = dr/dt \)とすると、
極座標による運動方程式は次式で表すことができます。
\begin{equation}
m\cfrac{dv}{dt} = -\cfrac{GMm}{r^{2}} \label{2-1}
\end{equation}
両辺に\(vdt/m\)をかけると
\begin{equation}
vdv = -\cfrac{GM}{r^{2}}vdt = -\cfrac{GM}{r^{2}}\cfrac{dr}{dt}{dt} = -\cfrac{GM}{r^{2}}{dr} \label{2-2}
\end{equation}
が得られます。上式の左辺、右辺をそれぞれ\(r=r_{0} \to \infty\)積分すると、
(左辺)
\begin{equation}
\int_{r_{0}}^{\infty} vdv = \int_{v_{0}}^{0} vdv = \Bigl[ \frac{1}{2} v^{2} \Bigr] ^{0}_{v_{0}} = -\frac{1}{2}{v_{0}}^{2} \label{2-3}
\end{equation}
(右辺)
\begin{equation}
\int_{r_{0}}^{\infty} -\cfrac{GM}{r^{2}}{dr} = \Bigl[ \cfrac{GM}{r} \Bigr] ^{\infty}_{r_{0}} = -\cfrac{GM}{r_{0}} \label{2-4}
\end{equation}
が得られるので、上記2式より
\begin{equation}
\frac{1}{2}{v_{0}}^{2} = \cfrac{GM}{r_{0}} \label{2-5}
\end{equation}
が得られます。上式より、
\begin{equation}
r_{0} = \cfrac{2GM}{{v_{0}}^{2}} \label{2-6}
\end{equation}
となるので、計算上、速度\(v_{0}\)が光速\(c\)に到達する距離\(r_{0}\)がシュバルツシルト半径\(R_{s}\)となります。
ただし、現実に落下速度が光速となるものではありません。
シュバルツシルト半径は、太陽では約3kmですが、巨大なブラックホールでは300km程度となります。
ここで、太陽の半径\(r_{sun}\)は約696,000kmであり、太陽のシュバルツシルト半径よりはるかに大きいです。
通常の恒星や衛星等の星も同様にその星の半径\(r\)はその星のシュバルツシルト半径\(R_{s}\)より大きくなります(\(r \gt R_{s}\))。
(3)シュバルツシルト計量の意義
計量テンソル\(g_{ij}\)は対称性があるので、一般的には独立項は10個ですが、
座標系が直交系のときはそのうち6個の成分は0となるため、独立項は4個となります。
ここで、この4個の独立項のうち変数\(\theta,\varphi\)に関する2つの成分\(g_{22},g_{33}\)は
重力方向に対して垂直であるため、処理が容易となります。
その結果、特別な成分は、時間軸方向\(ct\)の成分\(g_{00}\)と重力軸方向\(r\)の成分\(g_{11}\)の2つとなります。
以上も踏まえてシュバルツシルト計量の成分\(g_{ii}\)(\(i = 0,1,2,3\))を整理すると次のようになります。
①時間計量\(g_{t} = g_{00} = - \Bigl( 1 - \cfrac{R_{s}}{r} \Bigr) \)
恒星等に近いほど時間刻みが短くなるため、時間の進行が遅くなります。
②距離計量\(g_{r} = g_{11} = \Bigl( 1 - \cfrac{R_{s}}{r} \Bigr) ^{-1} \)
恒星等に近いほど目盛りが大きくなるため、長く見えます。
③計量\(g_{\theta} = g_{22} = r^{2} \)
④計量\(g_{\varphi} = g_{33} = r^{2}\sin^{2} \theta \)
シュバルツシルト計量はシュバルツシルト半径\(R_{s}\)を境界として次のように大きく異なります。
シュバルツシルト半径より内部の領域(\(r \lt R_{s}\))では、時間の微小変化\(dt\)による世界間隔の2乗\(ds^{2}\)が正(\(ds^{2} \gt 0\))となり、
\(t\)座標軸方向は時間的ではなく空間的(\(ds^{2} \gt 0\))となっています。
これに対して、\(r\)座標軸方向は、空間的ではなく時間的(\(ds^{2} \lt 0\))となっています。
6.2 シュバルツシルト半径より遠方領域の時空の性質
シュバルツシルト半径より遠方領域\(r \gt R_{s}\)のシュバルツシルト時空の性質を検討します。
(1) 重力による時間の遅れ
球対称な重力場を発生する物体(質料\(M\))の中心からの半径\(r\)が\(R_{s}\)より大きい位置(\(r \gt R_{s}\))
に静止して置いた時計の時間(固有時間\(\tau \))の進行の刻み\(d\tau \)は
\begin{equation}
-(cd\tau )^{2} = ds^{2} \label{f2-1-a}
\end{equation}
となります。
一方、無限遠方からミンコフスキー時空において漸近的に半径\(r\)位置へ接近するために
無限遠方に静止している座標系の観測者の時計の時間\(t\)の進行の刻みを\(dt\)とすると、
その座標系による計量\(ds^{2}\)は、\eqref{f1-3}より
\begin{equation}
ds^{2} = \Bigl(1-\cfrac{R_{s}}{r}\Bigr)(cdt)^{2} \label{f2-1-b}
\end{equation}
となるため、上記2式から次式が得られます。
\begin{equation}
d\tau = \sqrt{1 - \frac{R_{s}}{r}}\ dt \label{f2-1}
\end{equation}
したがって、無限遠方の観察者から重力場である\(r\)の位置においた時計の進行を観測すると、無限遠方の時間の進行より遅く観測されることになります。
例えば \(r = (4/3)R_{s}\) とすると、\eqref{f2-1}より、\(d\tau = (1/2)dt\) となるため、無限遠方の重力のない空間から観測すると、
重力のある空間の時計の進行は2分の1となり遅くなります。
この現象を「重力による時間の遅れ」といいます。
【コラム6】地球上の高さによる時計の進行
第3章の「3.2 地球上の高さによる時計の進行」において、
地上の床の時計Aから高さ\(H\)に置いた時計Bを観測すると、前記Ⅲ章(3)式に表さされるように時計Bは床の時計Aより早く進んでいるように観測されることとなります。
同(3)式は光のドップラー効果を利用して導出しましたが、同(3)式を本章によるシュバルツシルト計量にり導出した前記(13)式に基づいて導きたいと思います。
(13)式において、\(r\)を地球の地表面、\(H\)を地表面からの高さの位置とすると次式が得られます。 \[ d\tau = \sqrt{1 - \frac{R_{s}}{r + H}}\ dt \tag{c6-1} \] ここで、\(f(H)\)を \[ f(H) \equiv \sqrt{1 - \frac{R_{s}}{r + H}} \tag{c6-2} \] と定義すると、 \[ f'(H) = \cfrac{R_{s}}{2 (r+H)^{2}} \Bigl(1 - \frac{R_{s}}{r + H} \Bigr)^{-3/2} \tag{c6-4} \] であるから、\(H \ll r\)、\(R_{s} \ll r\)を考慮して、\(f(H)\)を\(H\)の1次の項まで級数展開により近似して得られた次式 \[ f(H) \doteqdot f(0) + f'(0)H = 1 + \cfrac{R_{s}}{2r^{2}}H = 1 + \cfrac{GM}{r^{2}} \cfrac{H}{c^{2}} \tag{c6-5} \] に、ニュートンの万有引力の法則(「第2章 曲がった空間」の(1)式))から誘導される\(GM/r^{2} = g\)(重力加速度)を代入すると \[ f(H) = 1 + \cfrac{gH}{c^{2}} \tag{c6-6} \] となるため、(c6-1)、(c6-2)、(c6-6)から次式が得られます。 \[ d\tau = f(H)dt = \Bigl( 1 + \cfrac{gH}{c^{2}} \Bigr)dt \tag{c6-7} \] ここで、この(c6-7)を3章(3)式と対比すると、(c6-7)の\(d\tau\)、\(dt\)がそれぞれ3章(3)式の\(\Delta T_{0}\)、\(\Delta T\) に対応しています。したがって、両式は一致していることがわかります。
(2) 重力による光の赤方偏移
前記のように無限遠方の観察者が強い重力場で時間の刻み幅\(dτ\)が無限遠方の固有時間の刻みdtより遅いと観測されるのは、
無限遠方では、強い重力場からの光の振動数が少なく、波長が長いものとして観測されるためです。
したがって、物体の中心から\(r\ \)の位置から固有振動数\(ν_{em}\)、固有波長\(λ_{em}\)で投光された光は、
無限遠方では次の振動数\(ν_{\infty}\)、波長\(λ_{\infty}\)の光として観測されます。
\begin{equation}
ν_{∞} = \sqrt{1 - \frac{R_{s}}{r}}\ ν_{em} \label{f2-2}
\end{equation}
\begin{equation}
λ_{∞} = \sqrt{1 - \frac{R_{s}}{r}}\ λ_{em} \label{f2-3}
\end{equation}
これにより、無限遠方で観測される光の波長が\(r\)の位置から投光する光の波長より長くなり、
光が赤方へ偏移することから、この現象を「重力による赤方偏移」といいます。
\eqref{f2-3}より、\(r\)が\(R_{s}\)に近づくと\(λ_{\infty}\)は無限大となるため、赤方偏移は無限大となります。
そこで、シュバルツシルト半径\(R_{s}\)の球面は”無限赤方偏移面”となります。
このことから、光源がシュバルツシルト半径内に入ると、そこから発した光は強い重力のために脱出できないことになります。
(3) 強い重力場における粒子の軌道
アインシュタインにより提案された一般相対性理論は実験(観測)データにより検証される必要があります。
しかし、地球上では強い重力場がありませんので、地球近辺で強い重力場として存在する太陽を利用して検証を行いました。
ニュートン力学で未解決であると第1章第1項で紹介した水星の近日点移動についての一般相対性理論で検証が行われました。
太陽の近傍は球対称な空間であるため、球対称な時空における粒子の極座標(\(r, \varphi\))で記述された軌道方程式(ただし、 \(u=1/r\))は次式で表されます。
\begin{equation}
(\frac{du}{d\varphi})^{2} + u^{2} = C + \frac{2GM}{q^{2}}u + R_{s}u^{3} \label{f3-1}
\end{equation}
ここで、\(C\)(積分定数)、\(q\)(単位質量あたりの角運動量(定数))は以下の通りです。
\begin{align}
&C = \frac{2}{q^{2}}(\frac{v^{2}}{2} - \frac{MG}{r}) \label{f3-3} \\
&v^{2} = \frac{(dr)^{2} + r^{2}(d\phi)^{2}}{(dτ)^{2}} \label{f3-4} \\
&q = r^{2}\frac{d\phi}{dτ} \label{f3-5}
\end{align}
なお、\eqref{f3-5}では、時間は粒子に固定した時計による時間(固有時間τ)で計測する必要があります。
ニュートン力学における惑星軌道の方程式である第1章の「1.1 水星の近日点移動」の(1)は、
\begin{equation}
(\frac{du}{d\varphi})^{2} + u^{2} = \frac{2GM}{q^{2}}u + C \label{f3-6}
\end{equation}
と変形できるため、\eqref{f3-1}をニュートン力学における惑星軌道方程式\eqref{f3-6}と対比すると、
\eqref{f3-1}は右辺第3項が追加されており、この第3項が重力を加味したものとなります。
この一般製相対性理論に基づいて惑星の中で太陽に最も近い位置にある水星の近日点移動についての計測データ
(水星の近日点移動参照)について太陽の重力の影響であることが実証されました。
なお、水星の近日点移動は100年間に574秒と微小ですので、惑星の公転移動(近日点移動)についての視覚的にわかりやすいシミュレーション結果を図2に示します。
従来のニュートン力学による惑星の公転軌道を赤線(\eqref{f3-6}による計算)、一般相対性理論による公転軌道(\eqref{f3-1}による計算)を青線で示しています。
ニュートン力学による軌道は太陽を1つの焦点として一定の楕円軌道となる(図2赤線、いわゆるケプラーの法則)のに対して、
一般相対性理論による軌道は、惑星が周回するごとにその軌道が少しずつずれていくことがわかります。
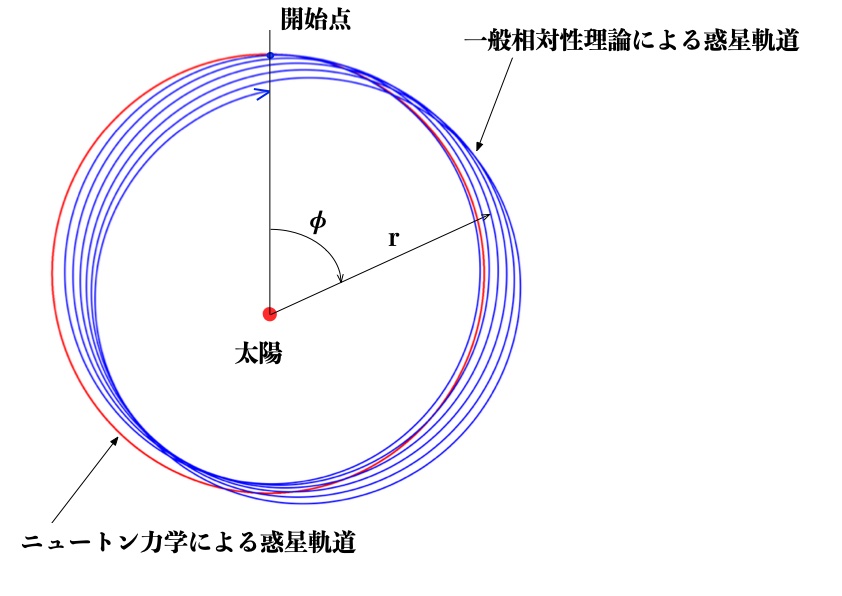
図2 重力の強い空間での惑星軌道(シミュレーション)
(4) 強い重力場における光跡の曲がり
最初の章で述べたニュートン力学で2つ目の未解決であった2.強い重力場での光の湾曲についての一般相対性理論で検証が行われました。
太陽の近傍は球対称な空間であるため、球対称な時空における光線の軌跡方程式は次式で表されます。
\begin{equation}
(\frac{du}{d\varphi})^{2} + u^{2} = C + R_{s}u^{3} \label{f3-7}
\end{equation}
ところで、原点を通るものを除く直線を極座標による微分方程式で表すと次式となることが知られています(図3)。
\begin{equation}
(\frac{du}{d\varphi})^{2} + u^{2} = \frac{a^{2} + b^{2}}{d^{2}} = C(定数) \label{f3-8}
\end{equation}
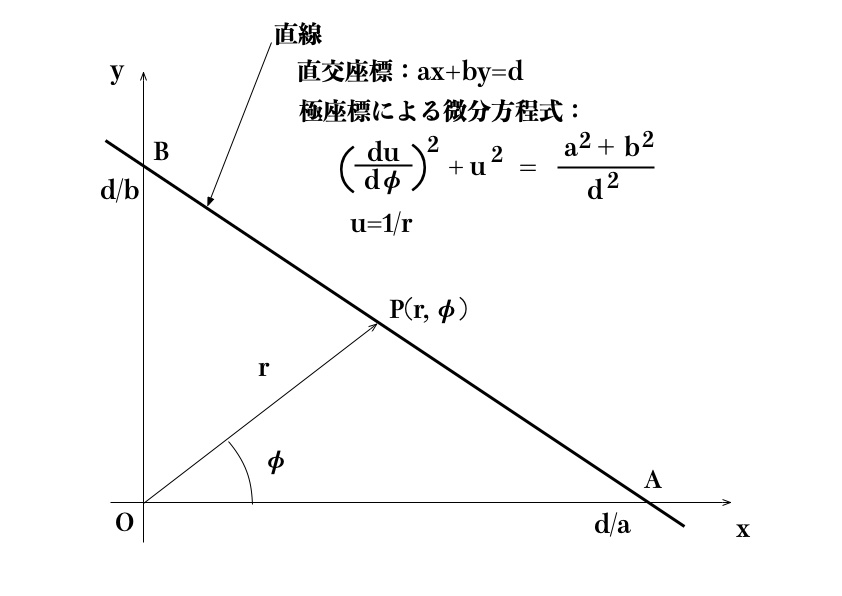
図3 直線を表す極座標微分方程式
したがって、\eqref{f3-7}は直線を表す\eqref{f3-8}の右辺に\(R_{s}u^{3}\)が追加されたものであり、
これにより、直線軌道から曲げられることがわかります。
この\eqref{f3-7}の右辺に追加された第2項は、強い重力源である太陽から離れる(\(r\)が大きくなる、
すなわち\(u=1/r\)が小さくなる)に従って小さくなるため、光跡は直線に近づくことになります。
光線の軌道方程式である\eqref{f3-7}を、質量を有する粒子の軌道方程式である\eqref{f3-1}と対比すると、
\eqref{f3-7}は\eqref{f3-1}右辺第2項 \(\Bigl( \cfrac{2GM}{q^{2}}u \Bigr) \) がないことがわかります。
\eqref{f3-7}から、太陽の重力による光跡の曲がり角度δを求めると近似的に次式で表されます(図4参照)。
\begin{equation}
\delta = 2\frac{R_{s}}{R_{0}} = C(定数) \label{f3-9}
\end{equation}
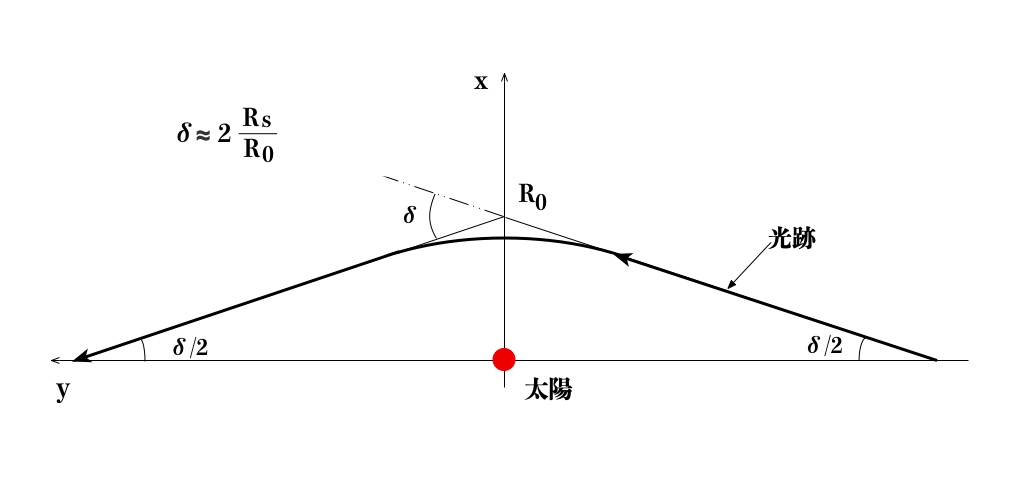
図4 光跡の曲がり角度δ
1919年にアフリカ西海岸で起きた日食で英国探検隊により観測されたデータと、アインシュタインが提案した一般相対理論に基づく計算値とが一致したことにより、
その正しさが立証されました。
【コラム7】重力レンズ
重力による光が曲がる作用を「重力レンズ」効果といい、天文学では重要な役割を果たしています。
最近は、電波を使うことにより日食を利用することなく、角度測定が行うことができ、例えば超長基線電波干渉計(VLBI)では、
クエーサーと呼ばれる天体からの電波を1%以下の精度で理論値と観測値の一致が得られています。
また、天体クエーサーと地球との中間に別の銀河が存在すると、重力レンズ効果により、クエーサーの像が点でなく、リング状に見えたりして非常に繊細な観測が可能となっています。
6.3 シュバルツシルト半径近傍での運動
シュバルツシルト半径\(R_{s}\)より遠方の\(r=r_{0}\) に静止していた粒子が\(r=R_{s}\) に落下していくとき粒子に固定した時計の時間(固有時間)\(τ\)は有限です。
すなわち、粒子は有限時間で \(r=R_{s}\)まで落下します。
しかし、無限遠方(重力の影響を受けない位置)から粒子の運動を観測すると、\eqref{f2-1}より、
粒子が\(r=R_{s}\) に近づくにつれ粒子に固定した時計の進行の刻み\(dτ\)が遅くなり無限に長い時間がかかるように見えます。
すなわち、無限遠方からは、粒子はシュバルツシルト半径\(R_{s}\)より内部には入らないように観測されます。
逆に、重力場から粒子が無限遠方に脱出する場合を考えます。
無限遠方での速度が0となるような\(r=r_{0}\)の位置での脱出速度\(v_{es}\)は次式で表されます。
\begin{equation}
v_{es} = c\sqrt{\frac{R_{s}}{r_{0}}} \label{g3-10}
\end{equation}
\eqref{g3-10}より、\( r = r_{0}=R_{s}\)での脱出速度\(v_{es}\)は光速度\(c\)となります。
このため、大きな質量の星等の天体が収縮によりその大きさがシュバルツシルト半径\(R_{s}\)より小さくなると、
その天体の強い重力のため、その天体のシュバルツシルト半径\(R_{s}\)の内部に入ると脱出が不可能となります。
このような天体がいわゆる「ブラックホール」と呼ばれており、
シュバルツシルト時空はそのようなブラックホールの1つです。