8 リーマン空間
一般相対性理論は、重力が作用する空間における物理現象を扱っています。
第1部で説明したとおり、重力が作用する空間においては、空間が重力の影響により曲がった空間となっており、
その曲がった空間に沿って物体が運動することになります。
リーマン幾何学は、アインシュタインが一般相対性理論の研究を行なっていた時代に、曲がった空間の幾何学として発展し、
アインシュタインが一般相対性理論を構築する際に参考、影響を受けているものであるため、
一般相対性理論をより深く理解するためには、リーマン幾何学についても基礎知識として理解しておくことが望ましいと考えられます。
しかし、リーマン幾何学を詳細に理解するのは難しいため、第1部においては、
理解の容易のため、曲がった空間について主として2次元曲面について説明しました。
一方、リーマン幾何学はより一般的な高次元の曲がった空間を対象としているため、
一般相対性理論の数学的基礎としては非常に有用となります。
そこで、本章では、一般相対性理論理解のための最小予備知識としてリーマン空間について紹介します。
8.1 計量テンソル
リーマン幾何学が対象とする空間をリーマン空間といい、距離が定義された空間です。
リーマン空間の次元に制限はありませんが、空間を表すための座標が必要であり、空間内のすべての位置は座標で特定できます。
n次元のリーマン空間の座標を(\(x^{1},x^{2},x^{3},・・・,x^{n}\))(\(\mu,\nu=1,2,3,・・・,n\))で表すこととすると、
座標値が微小異なる2点\(x^{\mu}\)と\(x^{\mu}+dx\)との間の距離\(ds\)が次式で定義されます(図1参照)。
\begin{align}
ds^{2} &= \sum_{\mu=1}^{n}\sum_{\nu=1}^{n}g_{\mu \nu}(x)dx^{\mu}dx^{\nu} \label{b1-1} \\
&= \sum_{\mu=1}^{n}\Bigl (\sum_{\nu=1}^{n}g_{\mu \nu}(x)dx^{\nu}\Bigr )dx^{\mu} \notag \\
&=
\begin{pmatrix}
g_{11} & g_{12} & \ldots & g_{1n} \\
g_{21} & g_{22} & \ldots & g_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
g_{n1} & g_{n2} & \ldots & g_{nn}
\end{pmatrix}
\begin{pmatrix}
dx^{1} \\
dx^{2} \\
\vdots \\
dx^{n}
\end{pmatrix}
\Bigl (dx^{1} \quad dx^{2} \quad \ldots \quad dx^{n} \Bigr ) \label{b1-2}
\end{align}
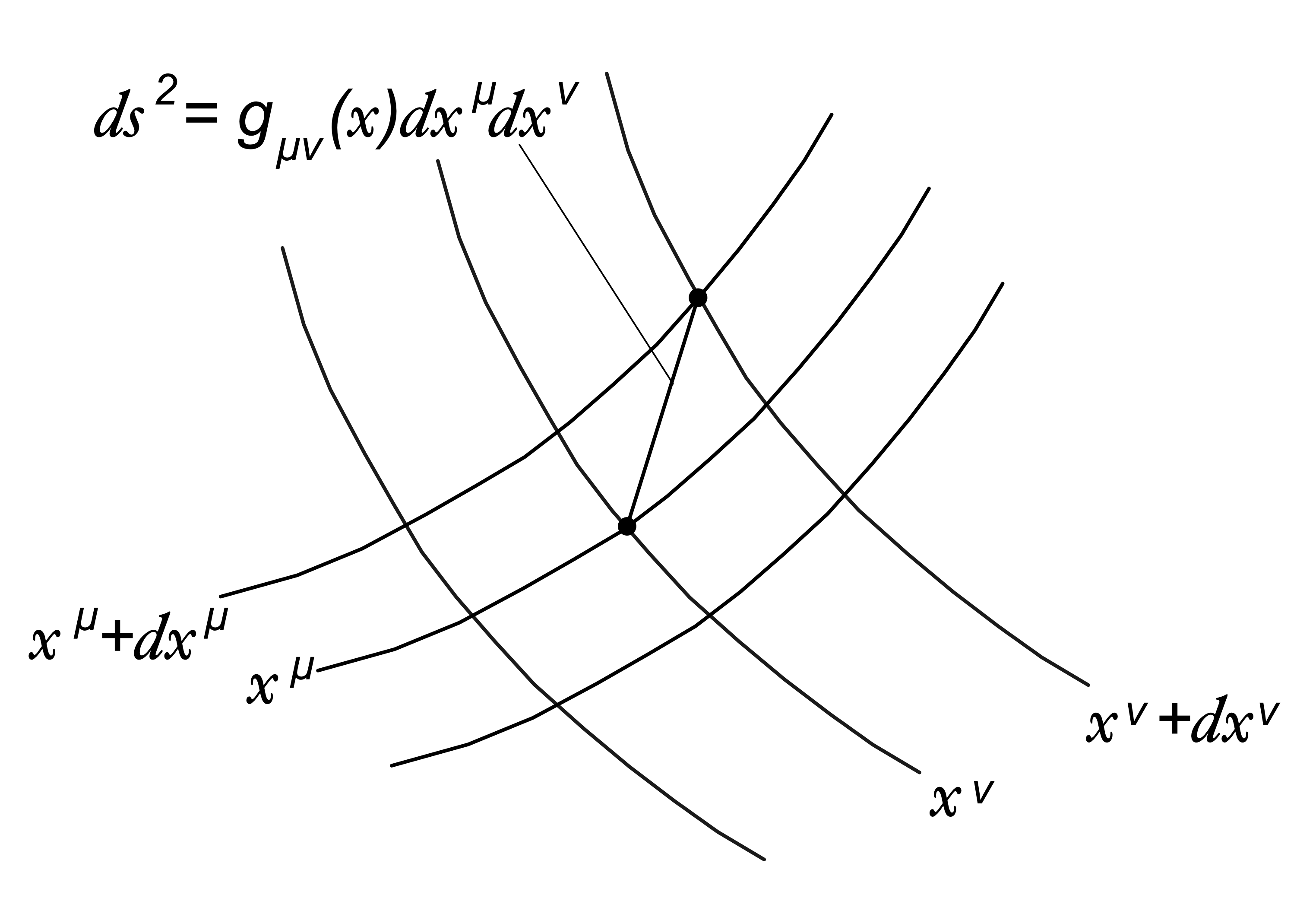
図1 リーマン空間
ここで、\(ds^{2}\)を計量、\(g_{\mu \nu}(x)\)を計量テンソルといい、
計量テンソルを行列で表すと次のようになります。
\begin{equation}
g_{\mu \nu} =
\begin{pmatrix}
g_{11} & g_{12} & \ldots & g_{1n} \\
g_{21} & g_{22} & \ldots & g_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
g_{n1} & g_{n2} & \ldots & g_{nn}
\end{pmatrix} \label{b1-3}
\end{equation}
これにより、距離\(ds\)は計量テンソル\(g_{\mu \nu}(x)\)により定義され、
計量テンソルにより空間の性質が特徴づけられることがわかります。
\eqref{b1-1}の右辺において、和記号\(\sum\)を頻繁に表記するのは煩わしいため、
数式の中の項に同じ添字が表記されているときは、特に断らない限り、
その添字について1からnの和を取るものとします(この表記法をアインシュタインの省略と呼びます)。
このアインシュタインの省略を利用すると、\eqref{b1-1}は次式のように簡略表記できます。
\begin{equation}
ds^{2} = g_{\mu \nu}(x)dx^{\mu}dx^{\nu} \label{b1-4}
\end{equation}
計量テンソルは対称とします(\(g_{\mu \nu}=g_{\nu \mu}\))。
その理由は、\(dx^{1}dx^{2}\)の成分は\((g_{12}(x)+g_{21}(x))dx^{1}dx^{2}\)としてまとめられ、
2つの和により距離が決まり、対称な成分は等しくしておくと便利だからです。
【例1】2次元平面
\begin{equation} ds^{2} = dx^{2} + dy^{2} = g_{\mu \nu}(x)dx^{\mu}dx^{\nu} \label{b1-5} \end{equation} \begin{equation} g_{\mu \nu}(x) = \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix} \label{b1-6} \end{equation} ここで、\(x^{1}\equiv x,\ x^{2}\equiv y\)(\(\mu,\nu=1,2\))
【例2】2次元球面
半径\(a\)の球面を座標\(\theta,\phi\)で表すと微小距離は
\begin{equation}
ds^{2} = a^{2}d\theta^{2} + a^{2}\sin^{2}\theta\ d\phi^{2}= g_{\mu \nu}(x)dx^{\mu \nu}dx^{\nu} \label{b1-7}
\end{equation}
\begin{equation}
g_{\mu \nu}(x) =
\begin{pmatrix}
a^{2} & \ \ 0\\
0\ \ & a^{2}\sin^{2}\theta
\end{pmatrix} \label{b1-8}
\end{equation}
ここで、\(x^{1}\equiv \theta,\ x^{2}\equiv \phi\)(\(\mu,\nu=1,2\))
【例3】ミンコフスキー時空
\begin{equation} ds^{2} = g_{ij}(x)dx^{i}dx^{j} \label{b1-9} \end{equation} \begin{equation} g_{ij}(x) = \eta_{ij} \label{b1-10} \end{equation} \begin{equation} \eta_{ij} = \begin{pmatrix} -1 & 0 & 0 & 0 \\ 0\ & 1 & 0 & 0 \\ 0\ & 0 & 1 & 0 \\ 0\ & 0 & 0 & 1 \end{pmatrix} \label{b1-11} \end{equation} ミンコフスキー時空では、3次元空間座標に時間座標\(ct\)を加えた4次元としているため、 \(x^{0}\equiv ct,\ x^{1}\equiv x,\ x^{2}\equiv y,\ x^{3}\equiv z\)(\(i,j=0,1,2,3\))としており、 \(\eta_{ij}\)を「ミンコフスキー空間の計量テンソル」といいます。
8.2 座標変換
(1)計量
リーマン空間の計量\(ds^{2}\)が座標系\(\bm x\)系で\(g_{\mu \nu}(x)\)を使用して
\begin{equation}
ds^{2} = g_{\mu \nu}(x) dx^{\mu}dx^{\nu} \label{b2-0}
\end{equation}
と表されているときに、別の座標系\( x' \)系では計量\( ds'^{2} \)として\( g_{\mu' \nu' }(x')\)で次式により表されていたとします。
\begin{equation}
ds'^{2} = g_{ \mu' \nu' }(x') dx^{ \mu' }dx^{ \nu' } \label{b2-1}
\end{equation}
この2つの座標系の変換式が一般座標変換
\begin{equation}
x^{\mu'} = f^{\mu}(x) \label{b2-2}
\end{equation}
とすると、曲率などの幾何学量が表現されるためには、この変換は1価連続、2階微分可能でなければなりません。
また、2点間の距離は座標系によらず同じ値であることは必要なため、\(ds^{2}=ds'^{2}\)より次式が成立する必要があります。
\begin{equation}
g_{\mu \nu}(x) dx^{\mu}dx^{\nu} = g_{\mu' \nu'}(x') dx^{\mu'}dx^{\nu'} \label{b2-3}
\end{equation}
上式より、計量テンソルの変換式は次式によることが示されます。
\begin{equation}
g_{\alpha' \beta'}(x') = g_{\mu \nu}(x)\dd{x^{\mu}}{x^{\alpha'}}\dd{x^{\nu}}{x^{\beta'}} \label{b2-4}
\end{equation}
(2)スカラー
リーマン空間の各点において、座標変換により値が変化しない物理量をスカラーといいます。
点Pは\(\bm x\)系ではP(\(x^{1},x^{2},x^{3},・・・\))、
\(\bm x'\)系ではP(\(x^{1'},x^{2'},x^{3'},・・・\))と定義します。
\(\bm x\)系では関数\(\Phi(x)\)が定義されているとき、\(\bm x'\)系に座標変換された関数を\(\Phi'(x')\)とすると、
次式が成立するとき、関数\(\Phi(x)\)をスカラーといいます。
\begin{equation}
\Phi'(x') = \Phi(x) \label{b2-5}
\end{equation}
(3)ベクトル
① 反変ベクトル
リーマン空間の隣接した2点間の座標値の差\(dx^{\mu}\)と同じ変換則に従って変換される量を反変ベクトルといいます。
一般座標変換式\eqref{b2-2}を\(x\)で微分すると、\(dx^{\mu}\)は次式で表される\(dx^{\mu'}\)に変換されます。
\begin{equation}
dx^{\mu'} = \sum_{\nu =1}^{n}\dd{x^{\mu'}}{x^{\nu}}dx^{\nu} \equiv \dd{x^{\mu'}}{x^{\nu}}dx^{\nu} \label{b2-6}
\end{equation}
上式を行列表記すると次式となります。
\begin{equation}
\begin{pmatrix}
dx^{1'} \\
dx^{2'} \\
\vdots \\
dx^{n'}
\end{pmatrix}
=
\begin{pmatrix}
\cfrac{\partial x^{1'}}{\partial x^{1}} & \cfrac{\partial x^{1'}}{\partial x^{2}} & ・・・ & \cfrac{\partial x^{1'}}{\partial x^{n}} \\
\cfrac{\partial x^{2'}}{\partial x^{1}} & \cfrac{\partial x^{2'}}{\partial x^{2}} & ・・・ & \cfrac{\partial x^{2'}}{\partial x^{n}} \\
\vdots & \vdots & \vdots & \vdots \\
\cfrac{\partial x^{n'}}{\partial x^{1}} & \cfrac{\partial x^{n'}}{\partial x^{2}} & ・・・ & \cfrac{\partial x^{n'}}{\partial x^{n}}
\end{pmatrix}
\begin{pmatrix}
dx^{1} \\
dx^{2} \\
\vdots \\
dx^{n}
\end{pmatrix} \label{b2-7}
\end{equation}
したがって、\(\bm x\)系におけるベクトル\(\bm{A}\)が次式に従って\(\bm x'\)系におけるベクトル\(\bm{A}'\)に変換されるとき、
ベクトル\(\bm{A}\)を反変ベクトルといいます。
反変ベクトルを示すために、座標軸の番号を示す添字を右肩に書きます。
\begin{equation}
A^{\mu'} = \dd{x^{\mu'}}{x^{\nu}}A^{\nu} \label{b2-8}
\end{equation}
なお、ベクトル\(\bm{A}\)からベクトル\(\bm{A}'\)への座標変換行列を\(\bm{C}\)とすると、
\begin{equation}
\bm{C} =
\begin{pmatrix}
\cfrac{\partial x^{1'}}{\partial x^{1}} & \cfrac{\partial x^{1'}}{\partial x^{2}} & ・・・ & \cfrac{\partial x^{1'}}{\partial x^{n}} \\
\cfrac{\partial x^{2'}}{\partial x^{1}} & \cfrac{\partial x^{2'}}{\partial x^{2}} & ・・・ & \cfrac{\partial x^{2'}}{\partial x^{n}} \\
\vdots & \vdots & \vdots & \vdots \\
\cfrac{\partial x^{n'}}{\partial x^{1}} & \cfrac{\partial x^{n'}}{\partial x^{2}} & ・・・ & \cfrac{\partial x^{n'}}{\partial x^{n}}
\end{pmatrix} \label{b2-9}
\end{equation}
となります。
② 共変ベクトル
スカラー場の勾配ベクトル\(\cfrac{\partial\Phi(x)}{\partial x^{\mu}}\)と同じ変換則に従って変換される量を共変ベクトルといいます。
\eqref{b2-5}を\(x^{\mu'}\)で微分すると、
\begin{equation}
\dd{\Phi'(x')}{x^{\mu'}} = \sum_{\nu=1}^{n}\dd{x^{\nu}}{x^{\mu'}}\dd{\Phi(x)}{x^{\mu}} \equiv \dd{x^{\nu}}{x^{\mu'}}\dd{\Phi(x)}{x^{\mu}} \label{b2-10}
\end{equation}
と変換されます。上式を行列表記すると次式となります。
\begin{equation}
\begin{pmatrix}
\cfrac{\partial}{\partial x^{1'}} \\
\cfrac{\partial}{\partial x^{2'}} \\
\vdots \\
\cfrac{\partial}{\partial x^{n'}}
\end{pmatrix}
\Phi'(x') =
\begin{pmatrix}
\cfrac{\partial x^{1}}{\partial x^{1'}} & \cfrac{\partial x^{2}}{\partial x^{1'}} & ・・・ & \cfrac{\partial x^{n}}{\partial x^{1'}} \\
\cfrac{\partial x^{1}}{\partial x^{2'}} & \cfrac{\partial x^{2}}{\partial x^{2'}} & ・・・ & \cfrac{\partial x^{n}}{\partial x^{2'}} \\
\vdots & \vdots & \vdots & \vdots \\
\cfrac{\partial x^{1}}{\partial x^{n'}} & \cfrac{\partial x^{2}}{\partial x'^{n}} & ・・・ & \cfrac{\partial x^{n}}{\partial x^{n'}}
\end{pmatrix}
\begin{pmatrix}
\cfrac{\partial}{\partial x^{1}} \\
\cfrac{\partial}{\partial x^{2}} \\
\vdots \\
\cfrac{\partial}{\partial x^{n}}
\end{pmatrix}
\Phi(x) \label{b2-11}
\end{equation}
ここで、\eqref{b2-5}を考慮すると、上式から次式が得られます。
\begin{equation}
\begin{pmatrix}
\cfrac{\partial}{\partial x^{1'}} \\
\cfrac{\partial}{\partial x^{2'}} \\
\vdots \\
\cfrac{\partial}{\partial x^{n'}}
\end{pmatrix}
=
\begin{pmatrix}
\cfrac{\partial x^{1}}{\partial x^{1'}} & \cfrac{\partial x^{2}}{\partial x^{1'}} & ・・・ & \cfrac{\partial x^{n}}{\partial x^{1'}} \\
\cfrac{\partial x^{1}}{\partial x^{2'}} & \cfrac{\partial x^{2}}{\partial x^{2'}} & ・・・ & \cfrac{\partial x^{n}}{\partial x^{2'}} \\
\vdots & \vdots & \vdots & \vdots \\
\cfrac{\partial x^{1}}{\partial x^{n'}} & \cfrac{\partial x^{2}}{\partial x^{n'}} & ・・・ & \cfrac{\partial x^{n}}{\partial x^{n'}}
\end{pmatrix}
\begin{pmatrix}
\cfrac{\partial}{\partial x^{1}} \\
\cfrac{\partial}{\partial x^{2}} \\
\vdots \\
\cfrac{\partial}{\partial x^{n}}
\end{pmatrix}
\label{b2-12}
\end{equation}
したがって、\(\bm x\)系におけるベクトル\(\bm{B}\)が次式に従って\(\bm x'\)系におけるベクトル\(\bm{B}'\)に変換されるとき、
ベクトル\(\bm{B}\)を共変ベクトルといいます。
共変ベクトルを示すために、軸の番号を示す添字を右下に書きます。
\begin{equation}
B_{\mu'}(x') = \dd{x^{\nu}}{x^{\mu'}}B_{\nu}(x) \label{b2-13}
\end{equation}
なお、ベクトル\(\bm{B}\)からベクトル\(\bm{B}'\)への座標変換行列を\(\bm{D}\)とすると、
\begin{equation}
\bm{D} =
\begin{pmatrix}
\cfrac{\partial x^{1}}{\partial x^{1'}} & \cfrac{\partial x^{2}}{\partial x^{1'}} & ・・・ & \cfrac{\partial x^{n}}{\partial x^{1'}} \\
\cfrac{\partial x^{1}}{\partial x^{2'}} & \cfrac{\partial x^{2}}{\partial x^{2'}} & ・・・ & \cfrac{\partial x^{n}}{\partial x^{2'}} \\
\vdots & \vdots & \vdots & \vdots \\
\cfrac{\partial x^{1}}{\partial x^{n'}} & \cfrac{\partial x^{2}}{\partial x^{n'}} & ・・・ & \cfrac{\partial x^{n}}{\partial x^{n'}}
\end{pmatrix} \label{b2-14}
\end{equation}
となります。
③ 反変ベクトルと共変ベクトルとの関係
\eqref{b2-9}、\eqref{b2-14}より次式が成立することがわかります。
\begin{equation}
\bm{C}^{T} = \bm{D}^{-1}
\end{equation}
\(\bm{A}'=\bm{C}\bm{A}\)の両辺の転置行列(\(\bm{A}'^{T}=\bm{C}^{T}\bm{A}^{T}\))
の両辺に左から\(\bm{B}'=\bm{D}\bm{B}\)をかけて、上式を利用すると
\begin{align}
\bm{A}'^{T}\bm{B} &= \bm{A}^{T}\bm{C}^{T}\bm{D}\bm{B} \notag \\
&= \bm{A}^{T}\bm{D}^{-1}\bm{D}\bm{B} \notag \\
&= \bm{A}^{T}\bm{B} \notag \\
&= A^{1}B_{1} + A^{2}B_{2} + \ldots +A^{n}B_{n} \label{b2-15}
\end{align}
となります。
したがって、反変ベクトル\(\bm{A}\)と共変ベクトル\(\bm{B}\)との内積\(\bm{A}^{T}\bm{B}\) はスカラー量となります。
(4)テンソル
2つの反変ベクトル\(A^{\mu}(x)\)、\(B^{\mu}(x)\)の成分の積がその\(\mu,\nu\)成分となっているテンソル
\begin{equation}
T^{\mu \nu}(x) = A^{\mu}(x)\cdot B^{\nu}(x) =
\begin{pmatrix}
A^{1}B^{1}\ A^{1}B^{2}\ ・・・ A^{1}B^{n} \\
A^{2}B^{1}\ A^{2}B^{2}\ ・・・ A^{2}B^{n} \\
\vdots\qquad\ \vdots\qquad\ \vdots\qquad\ \vdots \\
A^{n}B^{1}\ A^{n}B^{2}\ ・・・ A^{n}B^{n}
\end{pmatrix} \label{b2-16}
\end{equation}
について考えます。2つの添字をもつ\(T^{\mu \nu}\)のような量は2階のテンソルといい、
この\(T^{\mu \nu}\)は反変ベクトルの積であるため、座標変換により次式のように変換されます。
\begin{equation}
T^{\mu' \nu'}(x') = \dd{x^{\mu'}}{x^{\lambda}}\dd{x^{\nu'}}{x^{\sigma}}T^{\lambda \sigma}(x) \label{b2-17}
\end{equation}
このような変換をするテンソルを2階の反変ベクトルといいます。
同様に、2つの共変ベクトル\(A_{\mu}(x)\)、\(B_{\nu}(x)\)の積
\begin{equation}
T_{\mu \nu}(x) = A_{\mu}(x)\cdot B_{\nu}(x) \label{b2-18}
\end{equation}
は、共変ベクトルの積であるため、座標変換により次式のように変換されます。
\begin{equation}
T_{\mu' \nu'}(x') = \dd{x^{\lambda}}{x^{\mu'}}\dd{x^{\sigma}}{x^{\nu'}}T_{\lambda \sigma}(x) \label{b2-19}
\end{equation}
このような変換をするテンソルを2階の共変テンソルといいます。
同様に、1つの反変ベクトル\(A_{\mu}(x)\)と1つの共変ベクトル\(B_{\nu}(x)\)の積
\begin{equation}
{T^{\mu}}_{\nu}(x) = A^{\mu}(x)\cdot B_{\nu}(x) \label{b2-20}
\end{equation}
は、反変ベクトルと共変ベクトルの積であるため、座標変換により次式のように変換されます。
\begin{equation}
{T^{\mu'}}_{\nu'}(x') = \dd{x^{\mu'}}{x^{\lambda}}\dd{x^{\sigma}}{x^{\nu'}} {T^{\lambda}}_{\sigma}(x) \label{b2-21}
\end{equation}
このような変換をするテンソルを2階の混合テンソルといいます。
これらを拡張して、より任意の高階の反変テンソル、共変テンソル及び混合テンソルを定義することができます。
一般に、座標変換に対して次のように変換するテンソルをn階反変m階共変の混合テンソルといいます。
\begin{equation}
T^{a'b'\cdots}\ _{p'q'\cdots} = \dd{x^{a'}}{x^{\mu}}\dd{x^{b'}}{x^{\nu}}\cdots \dd{x^{u}}{x^{p'}}\dd{x^{v}}{x^{q'}}
\cdots T^{\mu \nu\cdots}\ _{uv\cdots} \label{b2-22}
\end{equation}
ここで、上添字\(a,b,\cdots\)の数はn個、下添字\(p,q,\cdots\)の数はm個です。