【問題1】
地球近くにいる宇宙船の中で生まれたばかりの子供(乳児)を乗せた宇宙船が地球から500光年離れた星に向かって出発した。
この子の寿命が現在の地球人と同様とした場合に、生存中に目的の星に到着できるか?
【解答(解説)】
ローレンツ収縮(第1部「\(Ⅲ\)基本原理から導かれる現象等」の「3.運動物体は運動方向の長さが収縮する」の式(9)により、速度\(v\)で移動する宇宙船から観測した目的の星までの距離Lは地球から観測された距離\(L_{0}\)より短くなる。
そのため、宇宙船内における子供の生存期間を\(T\)年とした場合に、短縮後の距離が\(L=u\) (光年/年) x \(T\) (年)より短くなれば、子供の生存中に目的の星に到達できる可能性がある。
\(v=βc\)であるから、式(9)より、
\[
β\ c\ T = L_{0}\ \sqrt{1-β\ ^{2}} \tag{A1-1}
\]
上式をβについて求めると、
\[
β\ = \cfrac{1}{\sqrt{1+(\cfrac{c\ T}{L_{0}})\ ^{2}}} \tag{A1-2}
\]
上式に、\(L_{0}=500\)光年、\(c=1\)光年/年、\(T\)=80年(平均寿命程度)を代入すると
\[
β\ = \cfrac{1}{\sqrt{1+(\cfrac{1\times 80}{500})\ ^{2}}}\ = 0.92848
\]
したがって、光速の92.9%以上の速度で宇宙船が飛行すれば、子供が生存している間に目的の星へ到達できる可能性がある。
《補足》
この問題の場合、その子供が目的の星に到着後しばらくして死亡して(宇宙船時計による死亡時の年齢80歳)、その事実の連絡を地球に電波等で送信すると、
地球ではその連絡を地球時計で送信の500年後(地球を出発してから1,000年後)に受信し、
その子供は(地球時計により)500歳まで生存したものとして記録される(第1部の「\(Ⅲ\)基本原理から導かれる現象等」の
「2.運動物体内の時間の進行が遅くなる」の最終段落参照)。
【問題2】 (双子のパラドックス)
双子の兄弟のうち、弟が地球に残り、兄が宇宙船に乗って速度\(v=0.6c\)(\(β=v/c=0.6\))で地球から9光年離れた星の近くまで行き、
そこで直ちに折り返して往きと同じ速度で地球に戻る宇宙旅行に行くこととなった。
兄が地球に戻り兄弟が再会するとき、静止している地球の時間に比べて宇宙船の時間の経過は遅くなるため、
宇宙船に乗った兄の方が歳をとるのが遅いことを理由に兄の方が若いと考えられる。
一方、宇宙船を基準(静止している)と考えれば、地球は宇宙船に対して運動しており、宇宙船内の時間より地球の時間の経過が遅くなるため、
地球に残った弟の方が歳をとるのが遅いことを理由に弟の方が若いと考えられる。
兄が地球に戻り兄弟が再会するとき、どちらが若いか?
【解答(解説)】
相互に一定の速度で運動する慣性系の間においては、一方の慣性系から他方の慣性系に固定された時計の経過を観測すると、
お互いに自分の時計より相手の時計の経過の方が遅いと観測される。
このため、弟がいる地球から兄の乗った宇宙船固定の時計を観測すると宇宙船固定の時計の進行の遅くなり、
兄の乗った宇宙船から地球固定の時計を観測すると地球固定の時計の進行の方が遅くなり、そのこと自体は正しく矛盾しない。
そのことから本問題は一見すると矛盾に見える「双子のパラドックス」として有名であるが、その原因を探求することが必要である。
1.結論
兄が地球に戻り兄弟が再開すると、兄の方が若い。
2.理由
この問題において兄弟で相違するのは、弟は最初から最後まで静止した地球にいるのに対して、
兄は方向転換を含む加減速により運動を行う宇宙船に乗って地球に戻るということである。
このため、宇宙船は全体として慣性系ではないため、弟がいる地球を静止した慣性系として考えることになる。
したがって、静止する地球に固定した時計に対して運動する宇宙船に固定した時計の経過時間が遅れるとして下記により求めた時間だけ兄の方が若くなる。
以下、その概要を以下に示す(本ページの<注1>一歩先の解説において紹介する)。
なお、宇宙船は、目的の星の近傍(折り返し点)にて、瞬時に速度を反転(\(v\)から\(-v\))するものとする。
(1) 宇宙船が地球を出発して折り返し点まで到着するまでの往路期間
① 地球時計による経過時間
宇宙船の巡航速度\(v\)は\(0.6c\)(0.6光年/年)であるため宇宙船自体の運動方向の長さはローレンツ収縮により短くなるが、
地球から折り返し点である星までの距離\(L_{0}\)は収縮せず9光年である。
したがって、地球に固定した時計による往路期間の経過時間\(T_{1}\)は、
\[
T_{1}=\frac{9\mathrm{(光年)}}{0.6\mathrm{(光年/年)}}=15\mathrm{年}
\]
である。
② 宇宙船時計による経過時間
速度\(v=0.6c\)(β=0.6)で巡航する宇宙船から観測する地球から目的の星までの距離Lは、ローレンツ収縮のため、本文ページの式(3)、(4)より
\begin{align}
&γ=\frac{1}{\sqrt{1-0.6^{2}}\ }=0.8\\[5pt]
&L=0.8\times 9(光年)=7.2\mathrm{(光年)}
\end{align}
と短くなる(第1部「\(Ⅲ\)基本原理から導かれる現象等」の「3運動物体の運動方向の長さが収縮する」のコラム3参照)。
したがって、宇宙船内に固定した時計による往路期間の経過時間\(t_{1}\)は
\[
t_{1} = 7.2\mathrm{(光年)/}0.6\mathrm{(光年/年)}= 12\mathrm{(年)}
\]
である。
(2) 宇宙船が折り返し点から地球に向けて出発して地球に到着するまでの復路期間
前項(1)と同様に地球時計の経過時間\(T_{2}\)は15年、宇宙船内時計の経過時間\(t_{2}\)は12年である。
(3) 往復期間(まとめ)
前項(1)、(2)より、宇宙船が目標の星近傍(折り返し点)まで往復して地球に戻るまでの経過時間\(T\)は地球時計で
\[
T = T_{1}+T_{2} = 15\mathrm{年}+15\mathrm{年} = 30\mathrm{年}
\]
であるのに対して、宇宙船内時計の経過時間\(t\)は
\[
t = t_{1}+t_{2} = 9\mathrm{年}+9\mathrm{年} = 18\mathrm{年}
\]
であり、宇宙船時計の経過時間の方が12年短い。
したがって、兄が宇宙旅行して地球に帰還し兄弟が再会したときの年齢は兄の方が12歳若いことになる(<注2>参照)。
この問題の事例のように宇宙船を使用した長期間の宇宙旅行により地球に帰還することは未来へのタイムトラベルとなる。
そこで、特殊相対性理論のこのような効果を日本では浦島効果と呼んでいる。
<注1>一歩先の解説
時空間等を利用した”もう一歩先の”解説を行う
(難しければ、先ず第2部「補説:もう一歩先へ」の「\(Ⅳ\)時空図」を参照)。
(1) 時空図
地球を静止座標系K、宇宙船を運動座標系K'とした時空図は図1の通りである。
地球座標系Kの中間点Mの同時刻線は点Mを通り地球座標系Kの\(x\)軸に平行な直線の上の世界点であるため、
地球座標系Kから観測したときに宇宙船座標系K'の折り返し点Rは地球座標系Kの中間点Mと同時刻となっている。
このため、地球座標系Kから宇宙船座標系K'を観測すると、宇宙船の軌跡は往復経路で相似形であることがわかる。
ただし、この時空図に示されるように、地球座標系Kと宇宙船座標系K'の時間はそれぞれの時計の固有時間τにより時間が経過するため、
兄が宇宙旅行から地球に帰還して兄弟が再会するまでの経過時間は弟(地球に滞在)が30年(往路時間\(T_{1}=\)復路時間\(T_{2}=\)15年)、
兄(宇宙船に搭乗)が24年(往路時間\(t_{1}=\)復路時間\(t_{2}=\)12年)である。
したがって、宇宙船に乗って地球に帰還する兄の方が地球に滞在している弟より経過時間が30年ー24年=6年短いため、兄の方が6歳若いこととなる。
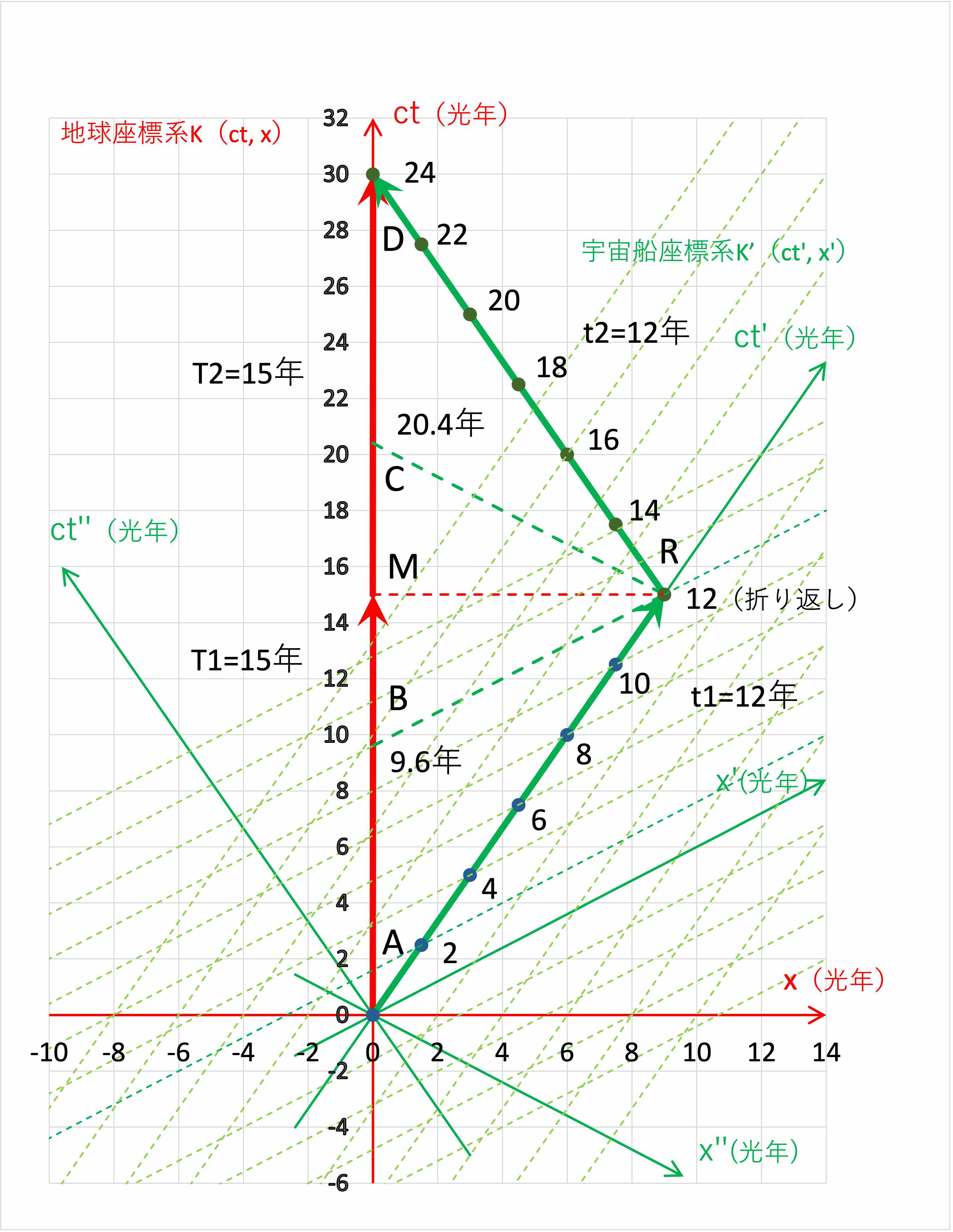
図1 時空図
《補足》 宇宙船座標系K'から地球座標系Kを観測することについて
宇宙船の折り返し点Rの到着時に宇宙船座標系K'から地球時計を観測すると、地球時計の経過時間は\(ct=9.6\)光年である。
宇宙船座標系K'における点Rの同時刻線は点Rを通りK'座標系のx'軸に平行な直線RB上の世界点であるため、
宇宙船座標系K'から観測したときに世界点Rと同時刻にあるのは(地球座標系K上の)世界点B(\(ct=9.6\)光年)であるからである。
これにより、往路において宇宙船から観測された地球固定時計の経過時間は\(ct=9.6\)光年(世界線ABに相当する経過時間)であり、
宇宙船時計の経過時間\(ct'=12\)光年(\(=ct/γ=0.8ct\))より5.4光年遅くなっている。
同様に、復路出発時点に宇宙船座標系K'から地球時計を観測すると、宇宙船座標系K'における世界点Rの同時刻線は世界点Rを通りK'座標系の\(x"\)軸に平行な直線RCであるため、
宇宙船座標系K'から観測したときに世界点Rと同時刻にあるのは(地球座標系K上の)世界点C(\(ct=20.4\)光年)である。
このため、復路において宇宙船から観測された地球時計の経過時間は\(ct=9.6\)光年(=30-20.4)(世界線CDに相当する経過時間)であり、
宇宙船時計の経過時間\(ct'=12\)光年(\(=ct/γ=0.8ct\))より5.4光年遅くなっている。
宇宙船座標系K'から観測された往路、復路の地球時計の経過時間を単純に加算すれば、地球時計の方が宇宙船時計の経過時間より10.8年遅くなる。
しかし、この計算では、地球時計における世界線BCの経過時間10.8光年(世界線BMとMCに相当する地球時計の経過時間の合計)が抜け落ちているという問題があり、誤りである。
宇宙船座標系K'から観測された地球時計の経過時間(世界線ABとCDに相当する地球時計の経過時間19.2光年)に、抜け落ちた地球時計の経過時間10.8光年を追加すれば、
当然のことながら地球時計の全経過時間30光年となります。
この宇宙座標系K'から観測された世界線BCの経過時間の抜け落ちは、座標系相互間の同時刻の相対性
(第1部の「\(Ⅲ\) 基本原理から導かれる現象等」の「「3.同時であることの相対性」及び第2部「もう一歩先へ」の「\(Ⅳ\) 時空図」」参照)
に起因しており、本解答の冒頭に書いたように宇宙船が途中で折り返して地球に戻ることが主たる原因である。
(2) 時空図その2
地球及び宇宙船の双方から一定期間(2年)間隔で信号(電磁波・光)を送信し、相手方は受信した信号に基づいて相互の時間の進行の確認を行うこととする。
その信号の送受信を表示した時空図は図2の通りである。
図2より、地球からの2年間隔の信号は往路では4年間隔、復路では1年間隔で宇宙船に届き、宇宙船からの2年間隔の信号は往路では4年間隔、復路では1年間隔で地球に届く。
信号の受信間隔が往復で異なるのは、往路では受信する信号(速度\(c\))から逃げるように両者が速度\(v=βc\)(本問題の場合、β=0.6)で離れて行く(両者の差は\(0.4c\))のに対して、
復路では受信する信号を迎えに行くように近づいて行くことに加えて、2年間隔の発信時点の両者の距離が往路では順次遠くなり(2年x0.6光年/年=1.2光年)、復路では順次近づくためである。
上の時空図により、お互いの時計に進行状況の確認ができ、これによっても兄弟が再開したとき、宇宙船時計の方が6年遅れていることがわかる。
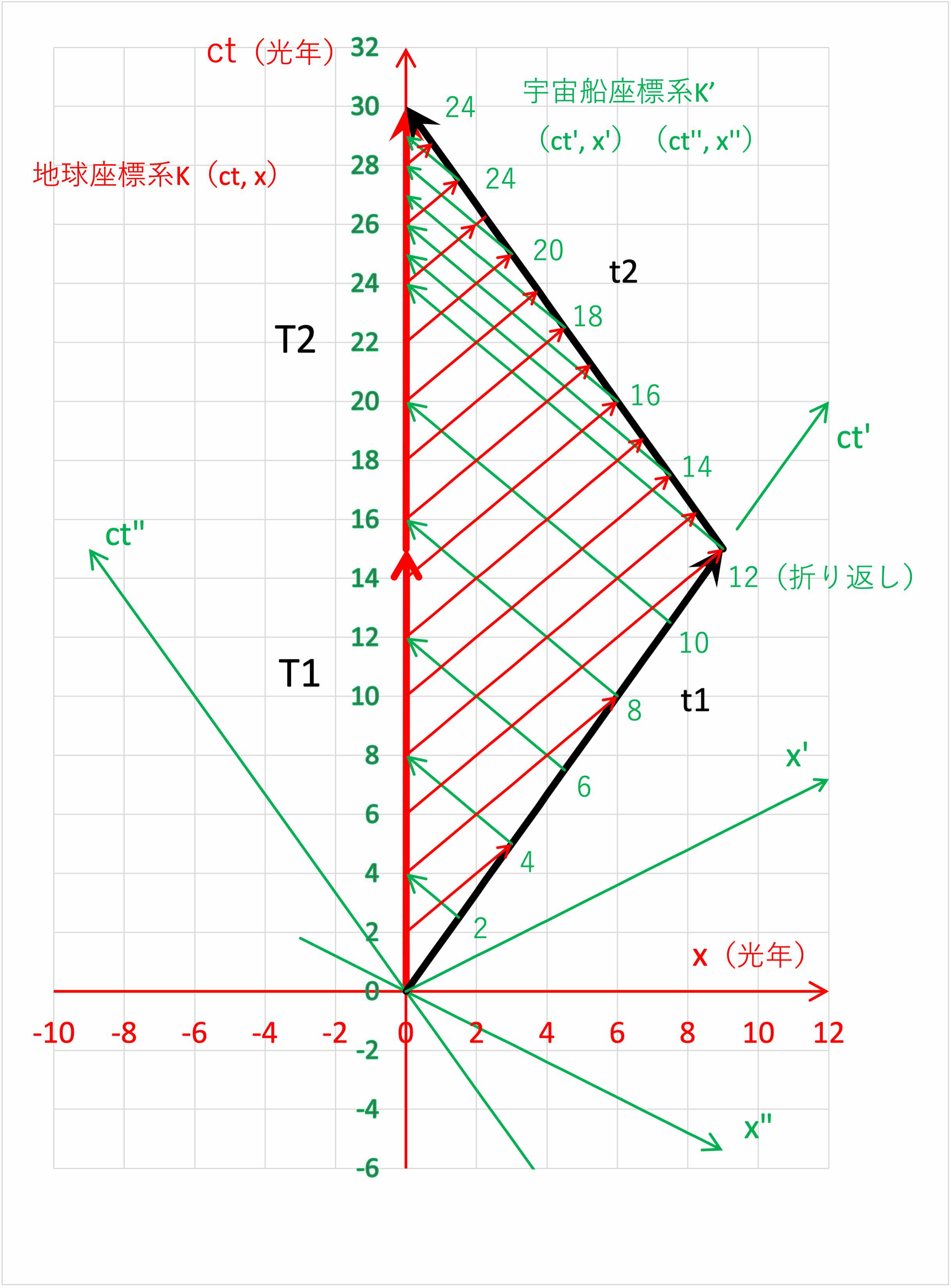
図2 時空図その2
<注2>宇宙線ミューオンの場合
第1部の「\(Ⅲ\) 基本原理から導かれる現象等」の「コラム2」、「コラム3」で
紹介した宇宙線ミューオンの地上への到達するまでの宇宙線ミューオン固定時計と地上時計との間の経過時間の相違が本問題2と類似なので、
改めて以下にて確認する。
高度5,000mでの宇宙線ミューオンの発生時刻と地上でのミューオンの発生時刻が同時とすると、宇宙線ミューオンと地上ミューオンが本問題におけるそれぞれ兄と弟に対応し、
宇宙線ミューオンが地上に到達した時にどちらの時計の経過時間の方が長かったかということになる。
高度5,000mで発生した宇宙線ミューオンが地上へ到達する時間はそれぞれ下記の通りである。
① 地上時計での経過時間\(t_{1}\)
\[
t_{1}=\frac{L}{0.99c}=\frac{5000\mathrm{(m)}}{0.99\x 3.00\x 10^{8}\mathrm{(m/sec)}}=16.8\ \mathrm{(μsec)}
\]
② 宇宙線ミューオン時計による経過時間\(t_{2}\)
\(t_{2}\) = 2.37μsec(第1部の「\(Ⅲ\) 基本原理から導かれる現象等」のコラム3)
以上①、②より、地上までの到達時間は、宇宙線ミューオン時計の場合は2.37μsecであるに対して地上ミューオン時計では16.8μsecである。
このため、宇宙線ミューオンが地上に到達した時点では、例えば寿命が3μsec(平均寿命2.2μsecより若干長い)のミューオンの場合、
宇宙線ミューオン(兄に対応)は消滅していないが、地上ミューオン(弟に対応)は宇宙線ミューオンの地上への到達のはるか前(寿命の約18%)に消滅している。
したがって、宇宙線ミューオンの場合も、本問題の解答と同様に、地上時計の方が進行が早いことが実証されている。