11 曲率とアインシュタインテンソル
11.1 リーマンの曲率テンソル
図1に示すように、球面の赤道上の点Rからベクトルが経線に沿って極点Pまで平行移動します。
次に、極点Pで点Rを通る経線に直角な経線に沿って極点Pから赤道上の点Sまでそのベクトルを平行移動させます。
さらに、そのベクトルを点Sから出発点Rに向かって赤道に沿って平行移動させて出発点Rに戻します。
このようなベクトルに平行移動をさせると、出発点Rにおいて出発時のベクトルの方向と戻り時のベクトルの方向が90°異なっています。
このように曲がった空間においては、ある領域を経路に沿って平行移動させて回り、
元の位置に戻ったときのベクトルの方向がどれだけずれるかによりその空間の曲がり具合を表現することができます。
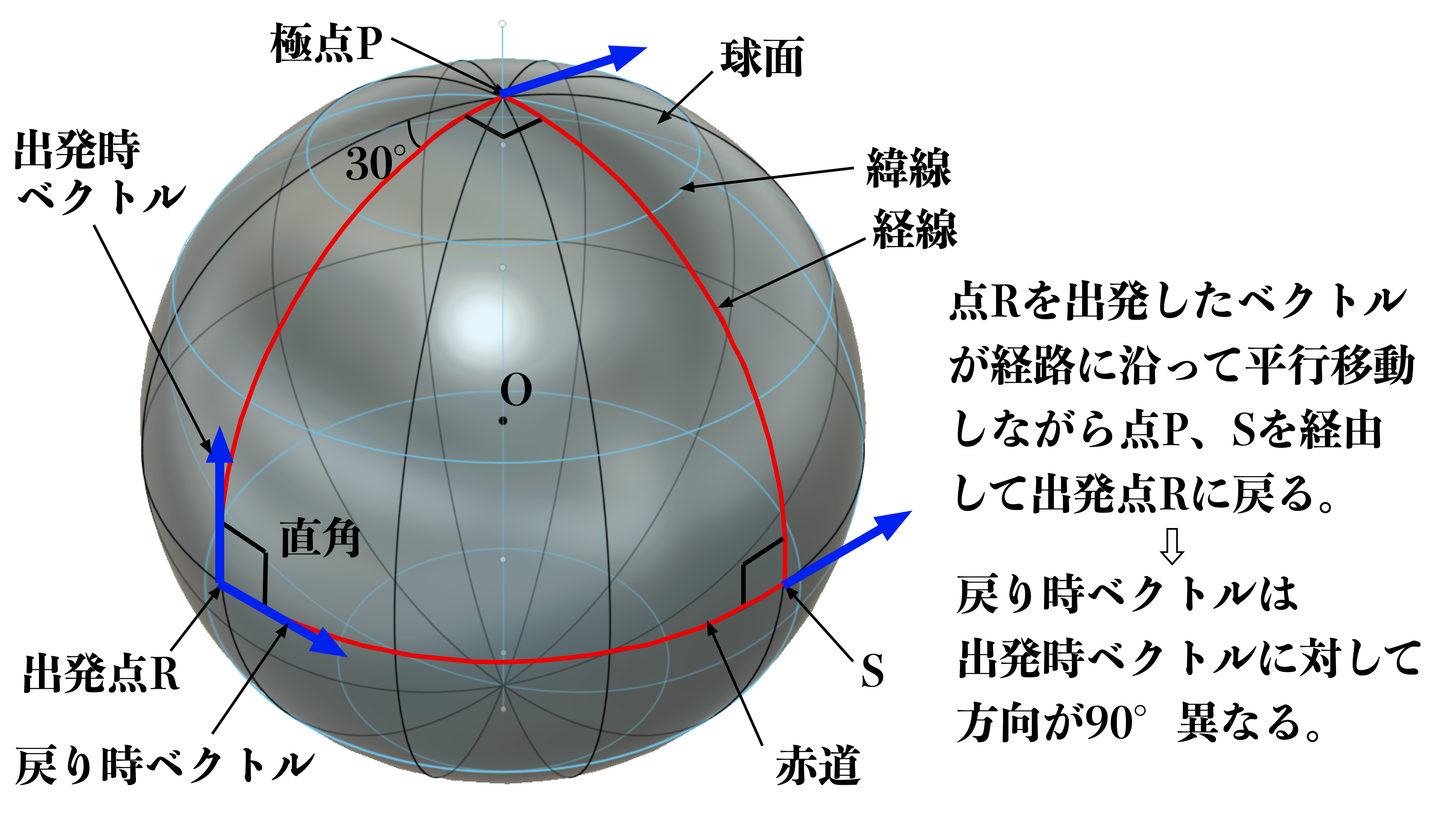
図1 球面上のベクトルの平行移動
図2に示す微小面積要素\(dx^{k}dx^{l}\)(ABCD)のまわりを、点Aのベクトル\(V^{i}\)が座標軸に沿って点B、C、Dの順に平行移動して
点Aに戻るとします。
ベクトル\(V^{i}\)が微小要素\(dx^{k}dx^{l}\)のまわりを回って点Aに戻ったときのベクトルを\(\tilde{V}^{i}\)とすると、
出発時のベクトル\(V^{i}\)との差\(\delta V\)は次式のとおりとなります。
\begin{equation}
\delta V = \Biggl(\dd{{\Gamma^{i}}_{kj}}{x^{l}} - \dd{{\Gamma^{i}}_{lj}}{x^{k}}
+ {\Gamma^{i}}_{lm}{\Gamma^{m}}_{kj} - {\Gamma^{i}}_{km}{\Gamma^{m}}_{lj}\Biggr) V^{j}dx^{k}dx^{l} \label{b5-1}
\end{equation}
ここで、
\begin{equation}
{R^{i}}_{jlk} \equiv \dd{{\Gamma^{i}}_{jk}}{x^{l}} - \dd{{\Gamma^{i}}_{jl}}{x^{k}}
+ {\Gamma^{i}}_{lm}{\Gamma^{m}}_{kj} - {\Gamma^{i}}_{km}{\Gamma^{m}}_{lj} \label{b5-2}
\end{equation}
とおくと、\eqref{b5-1}は次式となります。
\begin{equation}
\delta V = {R^{i}}_{jlk}V^{j}dx^{k}dx^{l} \label{b5-3}
\end{equation}
\eqref{b5-2}で定義される\({R^{i}}_{jlk}\)を「リーマンの曲率テンソル」又は「リーマンテンソル」といい、
ベクトルを微小面積要素のまわりを一周させたときに、戻ってきたときのベクトルが出発時のベクトルからのズレ量を示す量となります。
リーマン空間としての4次元時空がミンコフスキー空間であるための必要十分条件は、
リーマンの曲率テンソルの成分がすべて0であることです。
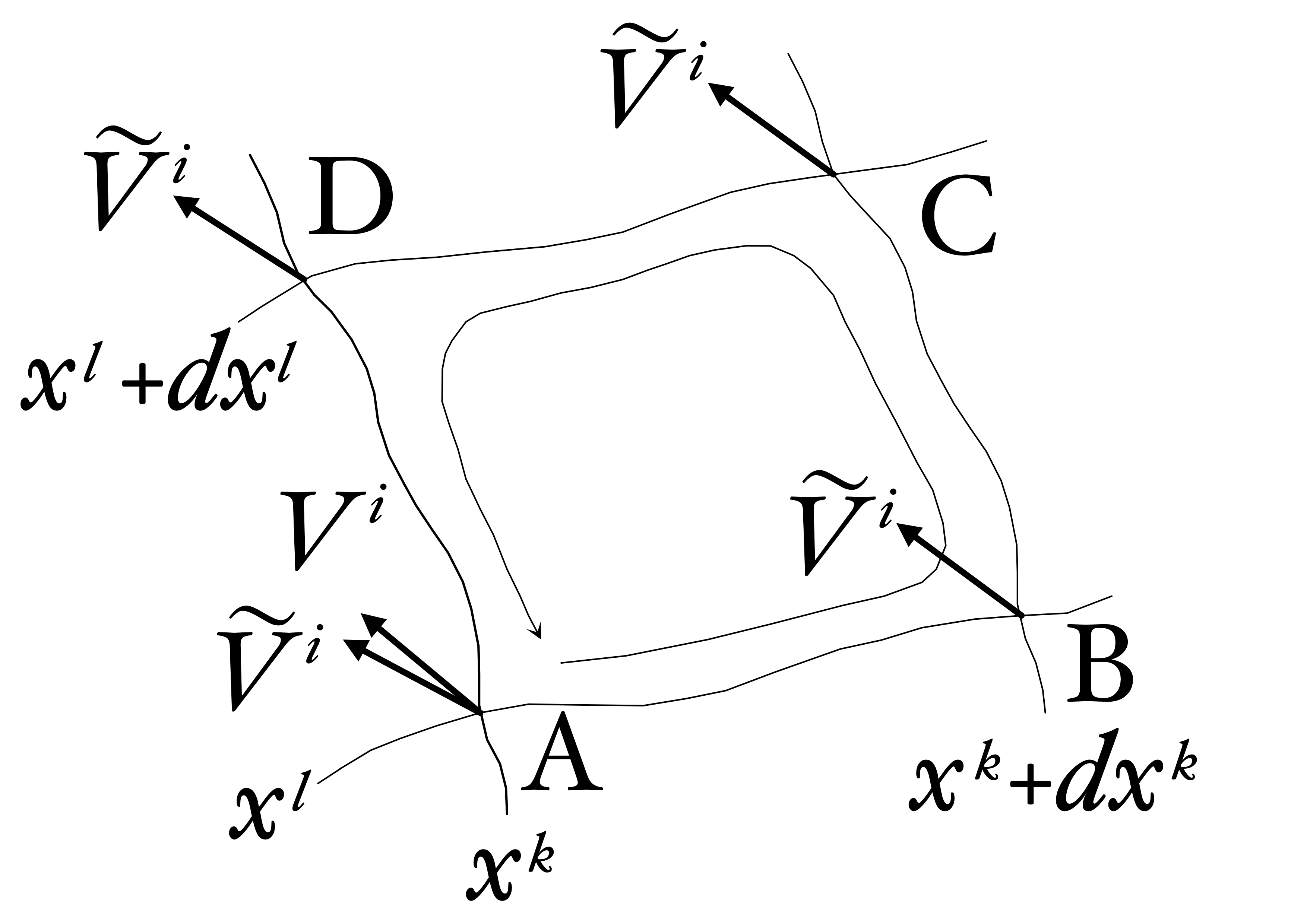
図2 微小面積要素まわりのベクトルの平行移動
11.2 リッチテンソル
リーマンの曲率テンソル\({R^{m}}_{nij}\)の第1添字と第3添字を縮約して作られる2階のテンソル
\begin{equation}
R_{nj} \equiv {R^{m}}_{nmj} \label{b5-4}
\end{equation}
を「リッチテンソル」といいます。
ここで、リッチテンソルをクリストッフェル記号をしようして次式のように表わすことができます。
\begin{align}
R_{nj} &= {R^{m}}_{nmj} \notag \\
&= \dd{{\Gamma^{i}}_{nj}}{x^{i}} - \dd{{\Gamma^{i}}_{ni}}{x^{j}}
+ {\Gamma^{a}}_{nj}{\Gamma^{i}}_{ai} - {\Gamma^{a}}_{ni}{\Gamma^{i}}_{aj}
\label{b5-5}
\end{align}
リッチテンソルは対称性(\(R_{ij}=R_{ji}\))をもっています。
11.3 スカラー曲率
リッチテンソルを縮約して作成された次式のスカラー量 \begin{equation} R = {R^{i}}_{i} \equiv g^{ij}R_{ij} \label{b5-6} \end{equation} を「スカラー曲率」といいます。
11.4 アインシュタインテンソル
次式で表される「ビアンキの恒等式」
\begin{equation}
\nabla_{k}{R^{m}}_{nij} + \nabla_{i}{R^{m}}_{njk} + \nabla_{j}{R^{m}}_{nki} = 0 \label{b5-7}
\end{equation}
に計量テンソル\(g^{kn}\)を乗じて下付き添字\(n\)を上付き添字に変えて(\( \because \ g^{ij}A_{n} = A^{n} \))
変更後の上付き添字\(n\)を\(k\)に変えて\(k\)について縮約をとると次式が得られます。
\begin{equation}
\nabla_{k}{R^{mk}}_{ij} + \nabla_{i}{R^{mk}}_{jk} + \nabla_{j}{R^{mk}}_{ki} = 0 \label{b5-8}
\end{equation}
上式をさらに、添字\(j\)を\(m\)に変えて\(m\)について縮約すると次式が得られます。
\begin{equation}
\nabla_{k}{R^{mk}}_{im} + \nabla_{i}{R^{mk}}_{mk} + \nabla_{j}{R^{mk}}_{ki} = 0 \label{b5-9}
\end{equation}
上式左辺第2項はスカラー曲率の定義より
\begin{equation}
\nabla_{i}{R^{mk}}_{mk} = \nabla_{i}R \label{b5-10}
\end{equation}
となります。
\eqref{b5-9}第3項において添字\(m\)を\(k\)に入れ換えてリーマンの曲率テンソルの対称性(\(R_{mnij}\) = \(-R_{nmij}\ ,\) \(R_{mnij}\) = \(-R_{mnji}\))
を用いると、第3項は第1項は等しくなるため、第1項と第3項の和は、縮約してリッチテンソルの定義を用いると
\begin{equation}
-2 \nabla_{k}{R^{mk}}_{im} = -2 \nabla_{k}{R^{k}}_{i} \label{b5-11}
\end{equation}
となります。
\eqref{b5-10}、\eqref{b5-11}を\eqref{b5-9}に代入して共変微分をまとめて整理すると次式が得られます。
\begin{equation}
\nabla_{k} {G^{k}}_{i} = 0 \label{b5-12}
\end{equation}
ここで、\({G^{k}}_{i}\)は次式で
\begin{equation}
{G^{k}}_{i} \equiv {R^{k}}_{i} - \cfrac{1}{2} {\delta ^{k}}_{i} R \label{b5-13}
\end{equation}
定義され、「アインシュタインテンソル」又は「アインシュタインの曲率テンソル」と呼ばれ、\eqref{b5-12}より発散が\(0\)であるテンソルです。
同様に、2階共変のアインシュタインテンソル\(G_{ij}\)が次式で定義されます。
\begin{equation}
G_{ij} \equiv g_{ik}{G^{k}}_{j}
= R_{ij} - \cfrac{1}{2} g_{ij} R \label{b5-14}
\end{equation}
2階半反変のアインシュタインテンソル\( G^{ij} \)も発散が\(0\)となります。
\begin{equation}
\nabla_{i} G^{ij} = 0 \label{b5-15}
\end{equation}
アインシュタインテンソルは、アインシュタインによって重量場の方程式の導出を行うために考え出されたものです。