10 共変微分
10.1 共変微分とクリストッフェル記号
平坦な空間に適用される通常の偏微分を曲がった時空における共変形式の偏微分に拡張したもの共変微分です。
共変ベクトル\( V_{i} \)を例にとると、\( j \)成分についての偏微分は次式により定義されます。
\begin{equation}
\dd{V_{i}(x)}{x^{j}} \equiv \lim_{\varDelta x^{j} \to 0} \frac{V_{i}(x+\varDelta x) - V_{i}(x)}{\varDelta x^{j}} \label{1-0}
\end{equation}
これに対して、\( j \)成分についての共変微分\( \nabla_{j}V_{i}(x) \)は
\begin{equation}
\nabla_{j}V_{i}(x) \equiv \lim_{\varDelta x^{j} \to 0} \frac{V_{i}(x+\varDelta x) - V_{i\, ||}(x+\varDelta x)}{\varDelta x^{j}} \label{1-1}
\end{equation}
と定義されます。ここで、ベクトル\( V_{i\, ||}(x+\varDelta x) \)は、図1に示すように、点Aにおける共変ベクトルを\( V_{i}(x) \)を点Bに平行移動したベクトルです。
なお、本サイトでは、共変微分の記号を\( \nabla \)の右下に座標を表示しますが、文献によっては、\( V_{i;j} \)のように
右下にセミコロン「;」付きの座標番号「\(j\)」を付けた添字として表示している場合もあります。
点Bにおけるベクトル\( V_{i}(x+\varDelta x) \)とベクトル\( V_{i\, ||}(x+\varDelta x) \)とは、
平坦な時空では一致するため\( \nabla_{j}V_{i}(x) = {\partial V_{i}}/{\partial x^{j}} \)となりますが、
曲がった時空では等しくなりません(\( \nabla_{j}V_{i}(x) \neq {\partial V_{i}}/{\partial x^{j}} \))。
そこで、ベクトル\( \tilde{V}_{i}(x+\varDelta x) \)のベクトル\(V_{i}(x)\)からの微小ズレ量\(\ \tilde{V}_{i}(x+\varDelta x) - V_{i}(x)\ \)
は、移動量\( \varDelta x^{j} \)の増減に比例して増減し、もともとのベクトル\( V \)の\( k \)成分の大きさ\( V \)に比例することから
微小ズレ量を\( \varDelta V_{k} \)とすると、比例係数を\( {\Gamma^{k}}_{ij} \)は次式のとおり定義できます。
\begin{equation}
V_{i\,||}(x+\varDelta x) = V_{i}(x) + \varDelta V_{k} \label{1-3}
\end{equation}
\begin{equation}
\varDelta V_{k} \equiv {\Gamma^{k}}_{ij}(x)V_{k}(x)\varDelta x^{j} \label{1-4}
\end{equation}
\eqref{1-3}、\eqref{1-4}を\eqref{1-1}に代入し、\eqref{1-0}を考慮すると
\begin{align}
\nabla_{j}V_{i}(x) &= \lim_{\varDelta x^{j} \to 0} \frac{ V_{i}( x+\varDelta x ) - {V}_{i}(x) - \varDelta V_{k} }{\varDelta x^{j}} \notag \\
&= \dd{V_{i}(x)}{x^{j}} - {\Gamma^{k}}_{ij}(x)V_{k}(x)
\label{1-5}
\end{align}
と得られます。
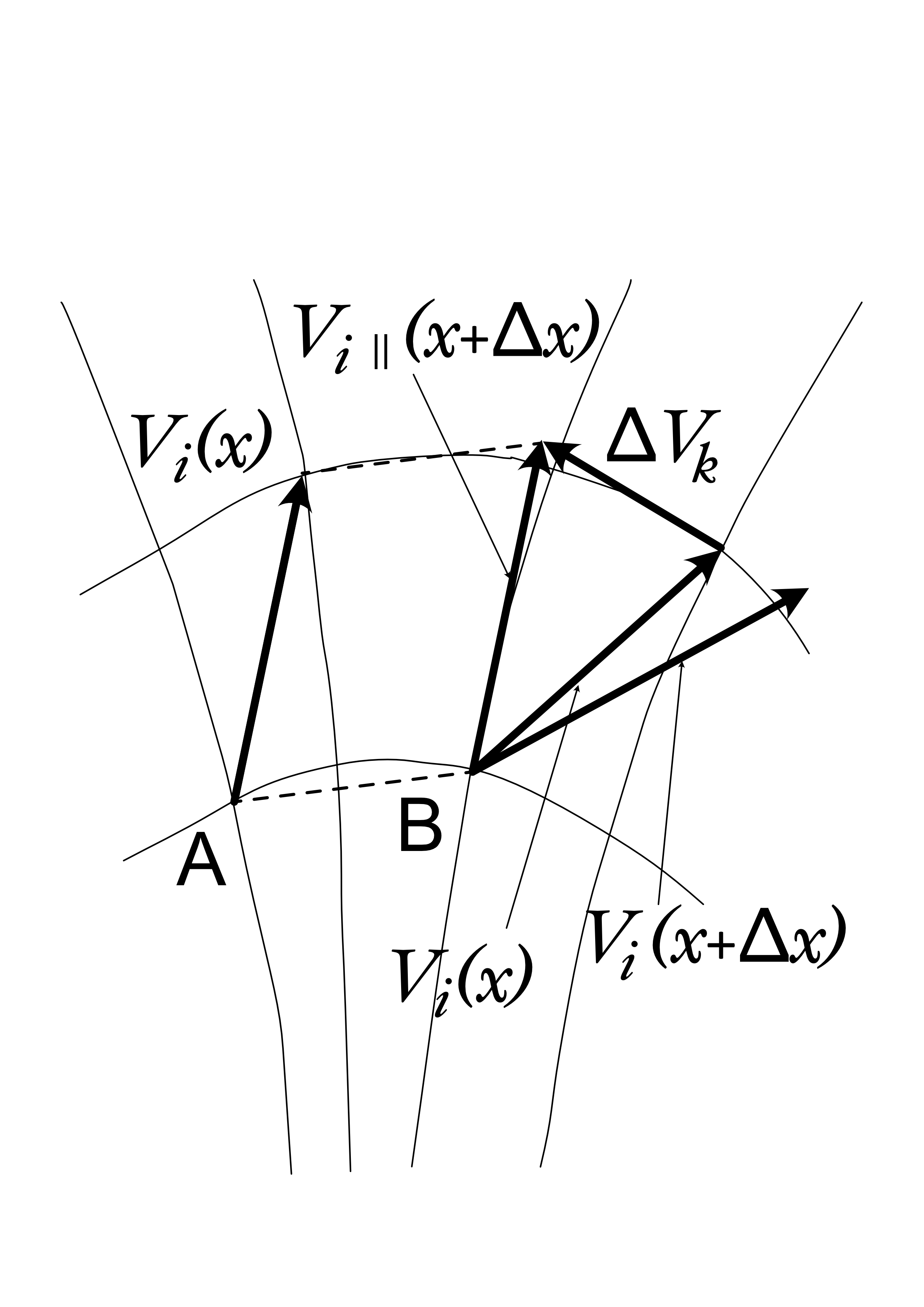
図1 一般座標系におけるベクトルの平行移動
上記で導入した比例定数\({\Gamma^{k}}_{ij}(x)\)を「クリストッフェル記号」と呼び、3つの添字を必要とし、一般相対性理論において重要かつ有用な量です。
右上の第1の添字\( k \)は微分される(基底)ベクトル、第2の添字\( i \)は微分する座標、第3の添字\( j \)は微分されてできたベクトルの成分を表します。
なお、クリストッフェル記号は対称性
\begin{equation}
{\Gamma^{k}}_{ij}(x) = {\Gamma^{k}}_{ji}(x) \label{1-8}
\end{equation}
があるため、局所的にクリストッフェル記号のすべての成分を座標変換によりゼロにでき、計量テンソル\( g_{ij} \)により
\begin{equation}
{\Gamma^{k}}_{ij}(x) = \frac{1}{2}g^{kl}\Biggl(\dd{g_{jl}}{x^{i}}+\dd{g_{li}}{x^{j}}-\dd{g_{ij}}{x^{l}} \Biggr) \label{1-9}
\end{equation}
と表わすことができます。
上記で定義された平行移動の性質は、ベクトルの長さが不変であることに加えて、次式で表されるように2つのベクトルの内積も不変となります。
\begin{equation}
g^{ij}(x+\varDelta x)A_{i\,||}(x+\varDelta x)B_{j\,||}(x+\varDelta x) = g^{ij}(x)A_{i}(x)B_{j}(x) \label{1-9-a}
\end{equation}
なお、偏微分記号\( \partial / \partial x^{j} \)の簡略表記として\( \partial_{j} \)が使用されることがあります。
この簡略表記を使用すると、通常の偏微分と共変微分との対応関係が
\begin{equation}
\partial_{j} \ \Longleftrightarrow \ \nabla_{j} \label{1-9-b}
\end{equation}
と明確になります。例えば、平坦な時空であれば、\eqref{1-5}において\( {\Gamma^{k}}_{ij} = 0 \)であるため、
\( \nabla_{j} V_{i}(x) = \partial_{j} V_{i}(x) \)となり、偏微分は共変微分の特別な場合ということがわかります。
【注1】等価原理の数学的表現
クリストッフェル記号\({\Gamma^{k}}_{ij}(x)\)は対称( \({\Gamma^{k}}_{ij}(x) = {\Gamma^{k}}_{ji}(x)\) )という性質は、
局所的にクリストッフェル記号\({\Gamma^{k}}_{ij}(x)\)のすべての成分を座標変換によりゼロ、すなわち
\begin{equation}
{\Gamma'^{k}}_{ij}(x) = 0 \label{1-10}
\end{equation}
とすることができることの必要十分条件となっています(証明省略)。
ここで、4章の4.2 弱い重力場中の粒子の運動方程式における(14)式において
重力または重力加速度に対応するものはクリストッフェル記号となり、クリストフェル記号\({\Gamma'^{k}}_{ij}(x) = 0\) であれば、
同(14)式右辺はゼロとなります。
このため、4次元時空において座標変換によって局所的にミンコフスキー時空が実現できることになります。
したがって、座標変換されて実現した局所的4次元時空は、当然慣性法則が成立している局所慣性系となるため、
\eqref{1-9}は等価原理に数学的表現となっています。
10.2 種々の量についての共変微分
共変微分は、簡単に言えば、一般の多変関数の偏微分に対応するものとなります。 したがって、一般の微分の公式の多くが共変微分にも同様に成立します。 一般相対性理論で取り扱う種々の量についての共変微分を以下説明します。
(1)スカラー
スカラーの微分\(\cfrac{\partial \phi(x)}{\partial x^{i}}\)は第8章第2項の「(3)ベクトル」の座標変換式である(21)式から共変ベクトルであるため、 スカラーの微分は共変量となっています。
(2)ベクトル
共変ベクトル\(V_{ij}(x) \)
共変ベクトル\( V_{i}(x) \)についての\( x^{k} \)に対する共変微分\( \nabla_{k}{V}_{i}(x) \)は、前項1の\eqref{1-9}のとおり
\begin{equation}
\nabla_{j}V_{i}(x) = \cfrac{\partial V_{i}(x)}{\partial x^{j}} - {\Gamma^{k}}_{ij}(x)V_{k}(x) \label{2-1}
\end{equation}
となります。
反変ベクトル\(V^{ij}\)
共変ベクトル\( A_{i}(x) \)の場合と同様に、反変ベクトル\(A^{i}(x) \)を点Bへ平行移動したベクトルを\( {A^{i}}_{||}(x+\varDelta x) \)とすると、
反変ベクトル\(A^{i}\)に対する共変微分\(\nabla_{k}{A}^{i}\)は
\begin{equation}
\nabla_{k}A^{i}(x) \equiv \lim_{\varDelta x^{k} \to 0}\frac{ A^{i}(x+\varDelta x) - {A^{i}}_{||}(x+\varDelta x)}{\varDelta x^{k}} \label{2-2-1}
\end{equation}
で定義され、点Bへ平行移動したベクトルを\( {A^{i}}_{||}( x + \varDelta x ) \)、比例係数\( {\Gamma^{i}}_{jk}(x) \)は、それぞれ次式のとおり表されます。
\begin{equation}
{A^{i}}_{||}(x+\varDelta x) = A^{i}( x ) + \varDelta A^{i} \label{2-2-2}
\end{equation}
\begin{equation}
\varDelta A^{i} = - {\Gamma^{i}}_{jk}(x) A^{k}(x) \varDelta x^{j} \label{2-2-3}
\end{equation}
したがって、\eqref{2-2-2}、\eqref{2-2-3}を\eqref{2-2-1}に代入すると
\begin{equation}
\nabla_{k}A^{i}(x) = \cfrac{\partial A^{i}(x)}{\partial x^{k}} + {\Gamma^{i}}_{jk}(x)A^{j}(x) \label{2-2-4}
\end{equation}
が得られます。
(3)テンソル
テンソルの共変微分は、重力場の方程式等の導入や処理において多用され重要なので、その公式等について、整理、紹介しておきます。
\begin{align}
\nabla_{k}(A_{i}B_{j}) &= \cfrac{\partial (A_{i}B_{j})}{\partial x^{k}} - {\Gamma^{m}}_{ik}A_{m}B_{j} - {\Gamma^{m}}_{jk}A_{i}B_{m} \label{b4-5-1} \\
&= \dd{A_{i}}{x_{k}}B_{j} + A_{i}\dd{B_{j}}{x^{k}} - {\Gamma^{m}}_{ik}A_{m}B_{j} - A_{i}{\Gamma^{m}}_{jk}B_{m} \notag \\
&= A_{i} \Big( \dd{B_{j}}{x^{k}} - {\Gamma^{m}}_{jk}B_{m} \Bigr) + \Bigl( \dd{A_{i}}{x_{k}} - {\Gamma^{m}}_{ik}A_{m} \Bigr) B_{j} \notag \\
&= A_{i}( \nabla_{k}B_{j} ) + ( \nabla_{k}A_{i} )B_{j}
\label{b4-5-2}
\end{align}
\eqref{b4-5-2}より、テンソル積の共変微分も、関数の積における次式のような通常の微分公式と同様な取り扱いができることがわかります。
\begin{equation}
\cfrac{d(fg)}{dx} = f \cfrac{dg}{dx} + \cfrac{df}{dx} g \label{b4-6-1}
\end{equation}
2階の共変テンソル\(T_{ij}\)
\begin{equation}
\nabla_{k}T_{ij} = \cfrac{\partial T_{ij}}{\partial x^{k}} - {\Gamma^{m}}_{ik}T_{mj} - {\Gamma^{m}}_{jk}T_{im} \label{b4-6-2}
\end{equation}
2階の反変テンソル\(T^{ij}\)
\begin{equation}
\nabla_{k}T^{ij} = \cfrac{\partial T^{ij}}{\partial x^{k}} + {\Gamma^{i}}_{km}T^{mj} + {\Gamma^{j}}_{km}T^{im} \label{b4-7}
\end{equation}
混合テンソル\( T^{ij}_{s} \)、\( T^{s}_{ij} \)
\begin{align}
& \nabla_{k} T^{ij}_{s} = \cfrac{\partial T^{ij}_{s}} {\partial x^{k}} + {\Gamma^{i}}_{km}T^{mj}_{s} + {\Gamma^{j}}_{km}T^{im}_{s}
- {\Gamma^{m}}_{sk}T^{ij}_{m} \label{b4-8} \\
& \nabla_{k} T^{s}_{ij} = \cfrac{\partial T^{s}_{ij}} {\partial x^{k}} + {\Gamma^{s}}_{mk}T^{m}_{ij} - {\Gamma^{m}}_{ik}T^{s}_{mj}
- {\Gamma^{m}}_{jk}T^{s}_{im} \label{b4-9}
\end{align}
計量テンソル\(g_{ij}\)
\begin{equation}
\nabla_{k}g_{ij} = 0 \label{b4-11}
\end{equation}
反変計量テンソル\(g^{ij}\)
\begin{equation}
\nabla_{k}g^{ij} = 0 \label{b4-12}
\end{equation}
したがって、計量テンソルは共変微分において定数として取り扱うことができます。